Non-integrability of the J₂₂-problem

The Theorem 1 by Yoshida presented in the previous section is useful to establish the non-integrability of Hamiltonian systems with homogeneous potential provided it has only two degrees of freedom. If it is not the case, other alternative procedures have to be used. In this line, Yoshida ([12]) obtained a criterion, also based on Ziglin's theorem ([14]), for the non-existence of an additional meromorphic integral in Hamiltonian systems with n degrees of freedom. Such a criterion can be stated as follows:

Theorem 2: Consider a Hamiltonian system with n degrees of freedom of the form

$$H = \frac{1}{2}{\bf p}^2 + V({\bf q})\, ,$$ (11)

where $V({\bf q})$ is assumed to be a homogeneous function of integer degree k ( $k\neq 0,\pm 2$). Since the equations of motion are scale-invariant, one can compute the Kowalevski exponents (KE), $\rho _1$, $\rho _2$, $\cdots$, $\rho _{2n}$ (see [8]). The KE characterize the branching of the solution in the complex t-plane as follows,

$${\bf q}(t)=t^{-g}\left[{\bf d}+\mbox{Taylor}(I_1t^{\rho _1},I_2t^{\rho _2},\cdots )\right]\, .$$ (12)

Here, g=2/(k-2), ${\bf d}$ is a constant vector, I_j are integration constants, and the term $\mbox{Taylor}(x, y, z, \cdots )$ denotes a convergent Taylor series. For (11), the KE have a pairing property, $\rho _i + \rho _{i+n}=2g+1$ $(i=1,2,\cdots ,n)$. Because of this pairing property, $\rho _i$ and $\rho _{i+n}$ can be rational numbers if and only if the difference $\Delta\rho _i:=\rho _{i+n}-\rho _i$ is a rational number. Further, one can always assume that $\Delta\rho _n$ is rational, $\Delta\rho _n=(3k-2)/(k-2)$.

Then, if the numbers $(\Delta\rho _1, \Delta\rho _2,\cdots , \Delta\rho _n)$ are rationally independent, then the Hamiltonian system (11) has no additional global analytic integral $\Phi ({\bf q},{\bf p})=const$ besides the Hamiltonian itself.

In general, it is quite obvious that the greater the number of degrees of freedom is, the more complicated the problem becomes. Moreover, let us point out that the analysis carried out through the above theorem is much more involved than that performed in the previous section, in which we only had to compute the integrability coefficient, while in the n-degrees of freedom criterion the knowledge of the eigenvalues of an n-dimensional matrix is required to determine the rational independence of the KE.

Next, we will consider the case for the satellite problem in which the only acting perturbation is that due to the term corresponding to the harmonic (2,2) of the development in spherical harmonics of the potential of the planet (i.e. the J₂₂-problem).

By using Cartesian coordinates in the rotating system Oxyz, attached to the rigid body, and which turns with uniform angular velocity $\omega$ with respect to the inertial axis, the Hamiltonian of the problem is

$$H_{s} = \frac{1}{2}\vert{\bf p}\vert^2 - \frac{\mu }{r} + V_{22} -\omega (xp_y -yp_x)\, ,$$ (13)

where

$$V_{22} = \frac{\textstyle\varepsilon (x^2-y^2)}{\textstyle r^......p_z^2\, ,\quad r = \vert{\bf q}\vert = \sqrt{x^2 + y^2 + z^2}$$

and the term $\omega (xp_y - yp_x)$ is due to the rotation of the reference frame.

Since the available non-integrability results are not directly applicable to the original problem (13), we first consider an auxiliary problem obtained by the reduction of the system deduced from (13) to a similarity invariant one. This system will be proved not to have additional meromorphic integrals by using the above quoted Theorem 2.

By performing the change of scale $(t, {\bf q}, {\bf p})\longrightarrow(\overline{t}, \overline{\bf q}, \overline{\bf p})$ defined by $t = \alpha ^{-1}\overline{t}$, ${\bf q} = \alpha ^{-2/5}\overline{\bf q}$, ${\bf p} = \alpha ^{3/5}\overline{\bf p}$ and taking limits when $\alpha\longrightarrow\infty$, the Hamiltonian (13) becomes

$$K_{s} = \frac{1}{2}(p_x^2 + p_y^2 + p_z^2) +\varepsilon\frac{\textstyle (x^2 - y^2)}{\textstyle r^5}\, ,$$ (14)

which is taken as Hamiltonian of an auxiliary problem.

Taking into account that (14) is of the type (11), with homogeneity degree k=-3, we can apply the Theorem 2. Since the algebraic equation $\mbox{\bf grad}\; V({\bf c})={\bf c}$ admits as solutions ${\bf c} = (0, \sqrt[5]{3\varepsilon }, 0)$ and ${\bf c} = (\sqrt[5]{-3\varepsilon }, 0, 0)$, we can compute the Hessian $V_{\bf qq}\left({\bf c}\right)$ and its eigenvalues to find that, in this case, $\Delta\rho _1=i\sqrt{31}/5$, $\Delta\rho _2=i\sqrt{15}/5$ and $\Delta\rho _3=11/3$. Therefore, as the imaginary numbers $i\sqrt{31}$, $i\sqrt{15}$ are rationally independent, the auxiliary Hamiltonian K_s (14) does not have any global meromorphic integral independent of the Hamiltonian.

Now, starting from the non-integrability of the auxiliary problem, we will try to get as much information as possible about the non-integrability of the original Hamiltonian (13). Let us remember that the forementioned theorem by Yoshida [12] is proved by using a particular straight-line solution of the form ${\bf q}(t)={\bf c}\cdot \phi (t)$, with $\phi (t)$ satisfying $\phi '' + \phi ^{k-1}=0$. Afterwards, the linear variational equations around that solution are set up. According to Ziglin's result [14], the problem is not integrable if two different non-resonant monodromy matrices (corresponding to suitable loops on a certain Riemann surface) not commuting can be found. In the case of homogeneous potential, the normal variational equations can be transformed into a Gauss hypergeometric equation and explicit expressions for the monodromy matrices are known (see [12]).

However, in our problem, the presence of the gyroscopic term in $\omega$ makes the aforementioned analysis more involved. In fact, it is not trivial to find a particular solution which, in the limit $\omega\longrightarrow 0$, tends to the straight-line solution used by Yoshida, which is decisive for calculating the monodromy matrices explicitly - apart from possible inconvenient variations of the Riemann surface and the necessary loops as $\omega$varies. So, alternative procedures should be used to ensure that (13) is not analytically integrable.

Nevertheless, what we can easily conclude is the non-existence of additional rational integrals in the original problem (13). Let us first note that if $\Phi ({\bf p}, {\bf q}, t) = const.$ is a rational first integral, by performing the forementioned change of variables, it becomes

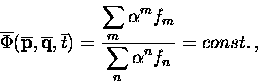$$\overline{\Phi }(\overline{\bf p},\overline{\bf q},\overlin......a ^{m}f_m}{\displaystyle\sum_{n}\alpha ^{n}f_n} = const.\, ,$$ (15)

where f_m and f_n are polynomials in $\overline{\bf p}$, $\overline{\bf q}$, t.

The expression (15) is a rational first integral of (13). Then, multiplying by an adequate power of $\alpha$ and taking limits when $\alpha\longrightarrow\infty$, we obtain a rational integral of the auxiliary problem (14).

Since (14) does not have any additional meromorphic integral, it cannot admit any additional rational integral and thus, neither does (13). Notice that the same assertion still holds if ${\bf q}$ gathers not only the Cartesian coordinates but also the radius r (or any other homogeneous function in the coordinates).

Another result, not formulated before, is the non-existence of any additional meromorphic integral without poles in z=0 and $\omega =0$ since, otherwise, the planar J₂₂-problem would have a meromorphic integral which is analytical in $\omega =0$. But this is impossible and can be easily deduced from Yoshida's results ([11], theorem 4.1). Moreover, we have the feeling that it could be quite difficult to have a spatial J₂₂-problem without the restriction of non-singularity in z=0 and $\omega =0$.

Let us remark that the case under study in this section is an example of sectorial truncation of the satellite problem (i.e. the problem of the satellite only perturbed by the main tesseral harmonic J₂₂). In this respect, new results concerning the non-integrability of sectorial and tesseral truncations of the satellite problem, when more suitable coordinates than the Cartesian ones are used, have been recently obtained by the authors and will be published in a forthcoming paper ([4]).