Next: Non-integrability of the J22-problem Up: Non-integrable cases in satellite Previous: Introduction
![]()
![]()
![]()
Next: Non-integrability
of the J22-problem Up: Non-integrable
cases in satellite Previous: Introduction
Let us begin by recalling a non-integrability criterion for 2-degrees of freedom Hamiltonian systems, with homogeneous potential of integer degree, obtained by Yoshida in 1987 [10]. Such a result is expressed as follows:
Theorem 1: Let ![]() be a homogeneous potential function of degree
be a homogeneous potential function of degree ![]() and compute the quantity (integrability coefficient)
and compute the quantity (integrability coefficient) ![]() defined by
defined by
| (1) |
where ![]() is the Hessian matrix of
is the Hessian matrix of ![]() and
and ![]() is a solution of the algebraic equation
is a solution of the algebraic equation ![]() .
.
If ![]() is in the so-called non-integrability regions Sk, then
the 2-degrees of freedom Hamitonian system
is in the so-called non-integrability regions Sk, then
the 2-degrees of freedom Hamitonian system ![]() is non-integrable, i.e. there cannot exist an additional integral
is non-integrable, i.e. there cannot exist an additional integral ![]() which is complex analytic in
which is complex analytic in ![]() .
.
For our purposes, it suffices to consider ![]() and the Sk given by
and the Sk given by
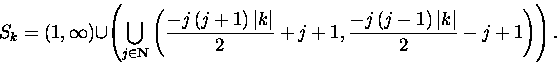 |
(2) |
Now, let us consider the Hamiltonian of the truncated zonal satellite
of order ![]() in Cartesian canonical variables
in Cartesian canonical variables ![]()
| |
(3) |
where
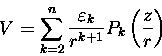 |
(4) |
is the disturbing potential, Pk(x) is the Legendre
polynomial of order k, ![]() and
and ![]() are coefficients which can be considered as small parameters.
are coefficients which can be considered as small parameters.
If we carry out a change to cylindrical variables ![]() the
Hamiltonian (3) is transformed into
the
Hamiltonian (3) is transformed into
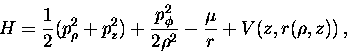 |
(5) |
where ![]() and
and ![]() the vertical component of the angular momentum, is a first integral since
the coordinate
the vertical component of the angular momentum, is a first integral since
the coordinate ![]() is ignorable.
is ignorable.
The Hamiltonian (5) has the integrals H=
const. and ![]() const., which are independent and are in involution (i.e. the Poisson bracket
const., which are independent and are in involution (i.e. the Poisson bracket
![]() ).
Let us suppose that there exists a third first integral F, independent
of the other two and in involution with them, that is, verifying
).
Let us suppose that there exists a third first integral F, independent
of the other two and in involution with them, that is, verifying ![]() since
since ![]() always holds provided F is a first integral.
always holds provided F is a first integral.
As ![]() ,
it is obvious that F does not depend on
,
it is obvious that F does not depend on ![]() .
If we perform the reduction of order of the Hamiltonian (5),
by considering
.
If we perform the reduction of order of the Hamiltonian (5),
by considering ![]() as
a parameter, it is clear that if (5) is completely
integrable with integrals H,
as
a parameter, it is clear that if (5) is completely
integrable with integrals H, ![]() and F, the reduction will also be so with integrals
and F, the reduction will also be so with integrals ![]() and
and ![]() .
Likewise, if the integrals of (5) are meromorphic,
so are those of the reduction. Moreover, we can assume that F is
analytical in
.
Likewise, if the integrals of (5) are meromorphic,
so are those of the reduction. Moreover, we can assume that F is
analytical in ![]() since otherwise it suffices to multiply F by a suitable power of
since otherwise it suffices to multiply F by a suitable power of
![]() ,
as
,
as ![]() is a first integral
is a first integral ![]() because
because ![]() and F are so. In consequence, if (3)
is Liouville integrable, so is
and F are so. In consequence, if (3)
is Liouville integrable, so is
| |
(6) |
which is obtained by making ![]() in the reduction of (5) to two degrees of
freedom.
in the reduction of (5) to two degrees of
freedom.
Notice that, as the potential of this 2-degrees of freedom Hamiltonian
consists of a finite number of homogeneous terms, whose degrees vary from
-1 (corresponding to the Keplerian term) to -n-1, we are in conditions
to apply the Yoshida theorem ([11], theorem
4.1), which allows us to establish the non-existence of an additional meromorphic
integral if the integrability coeficient ![]() of either the lowest or highest order part is in their corresponding non-integrability
regions. To this end, proceeding as Yoshida [9],
by performing a suitable change of scale, the Hamiltonian (6)
becomes
of either the lowest or highest order part is in their corresponding non-integrability
regions. To this end, proceeding as Yoshida [9],
by performing a suitable change of scale, the Hamiltonian (6)
becomes
| |
(7) |
which is taken as Hamiltonian of an auxiliary problem (see [2] for details).
As the potential Vn is homogeneous of order m=-n-1,
according to Theorem 1, the non-existence of any other meromorphic
integral simply depends on finding a solution ![]() of the algebraic equation
of the algebraic equation
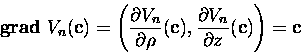 |
(8) |
and on the value of the integrability coefficient ![]() defined by
defined by
| |
(9) |
It is easily checked that the system (8)
admits a solution of the form ![]() ,
where z0 is a solution to the equation
,
where z0 is a solution to the equation
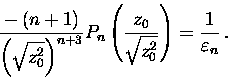 |
(10) |
On the other hand, by using well known properties of Legengre polynomials,
straightforward calculations allow us to compute the trace ![]() to find that the integrability coefficient
to find that the integrability coefficient ![]() is
is
![]()
As the non integrability regions S-n-1 defined
in (2) contain the interval ![]() ,
we conclude that the auxiliary Hamiltonian (7)
is non-integrable.
,
we conclude that the auxiliary Hamiltonian (7)
is non-integrable.
Now, coming back to the Hamiltonian (6), according to Yoshida ([11], theorem 4.1), in our case, it holds for the lowest order -n-1 and hence (6) is non-integrable. In consequence, as explained before, the original problem (5) is not Liouville integrable through meromorphic integrals.
Let us remark that the choice of the solution to (8) carried out here has allowed us to prove the non-integrability of any truncation of the zonal satellite problem irrespective of whether it ends in even or in odd harmonics, while the solution chosen by Irigoyen and Simó [3] to set up the non-integrability of the J2-problem (whose truncation ends in J2) would only be useful to prove the non-integrability of truncations ending in even harmonics.