Next: The General Main Satellite Up: NON-INTEGRABILITY OF THE MOTION Previous: Brief Summary of Yoshida's
![]()
![]()
![]()
Next: The
General Main Satellite Up: NON-INTEGRABILITY
OF THE MOTION Previous: Brief
Summary of Yoshida's
In this section we present some results about this problem recently obtained by the authors [2], although the proof has been considerably shortened.
By using cylindrical coordinates ![]() ,
the homogeneous Hamiltonian for this problem can be written as
,
the homogeneous Hamiltonian for this problem can be written as
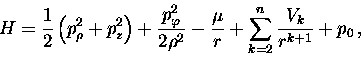 |
(1) |
where ![]() ,
,
![]() ,
,
![]() are constant and Pk(x) is the Legendre polynomial
of order k.
are constant and Pk(x) is the Legendre polynomial
of order k.
From the fact that ![]() is a first integral of (1) it follows that,
if this Hamiltonian admits a meromorphic integral independent from the
other two and in involution with them, such an integral is analytic with
respect to
is a first integral of (1) it follows that,
if this Hamiltonian admits a meromorphic integral independent from the
other two and in involution with them, such an integral is analytic with
respect to ![]() .
Consequently, the integrability in the Liouville sense of (1)
implies that of the Hamiltonian
.
Consequently, the integrability in the Liouville sense of (1)
implies that of the Hamiltonian
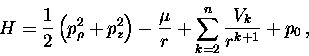 |
(2) |
which is obtained by making ![]() in (1). It is immediate that (2)
admits a particular solution with
in (1). It is immediate that (2)
admits a particular solution with ![]() .
However, since an explicit expression for the associate monodromy matrices
which are required by Ziglin's method is not known, it is convenient to
introduce a suitable limit problem.
.
However, since an explicit expression for the associate monodromy matrices
which are required by Ziglin's method is not known, it is convenient to
introduce a suitable limit problem.
The change of scale defined by
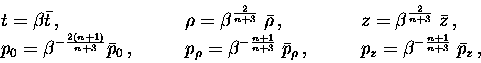
gives a new homogeneous Hamiltonian, which after multiplying by 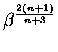 and taking limits as
and taking limits as ![]() ,
reduces to
,
reduces to
| |
(3) |
and the bar in the new variables has been removed to simplify the notation.
The Hamiltonian (3) is of the form required
by Yoshida's theorem [11], since the potential
V is homogeneous of degree k=-n-1. As is well known,
the Hessian of V computed on the vector ![]() quoted in section 2 always has the eigenvalue k-1, which in our
case turns out to be -n-2. It is easy to establish that this is
precisely the value of
quoted in section 2 always has the eigenvalue k-1, which in our
case turns out to be -n-2. It is easy to establish that this is
precisely the value of ![]() ,
so that the integrability coefficient reduces to
,
so that the integrability coefficient reduces to ![]() .
Moreover, due to the symmetry with respect to the OZ axis, it is
obvious that
.
Moreover, due to the symmetry with respect to the OZ axis, it is
obvious that
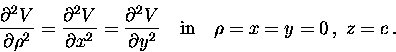
Since V verifies Laplace equation, we get
![\begin{displaymath}\left.\displaystyle\frac{\partial ^2V}{\partial\rho ^2}\rig......\ [-.2cm]z = c\end{array}} = 1+\displaystyle\frac{n}{2}\, ,\end{displaymath}](img35.gif)
a value which lies in the non-integrability region S-n-1 and coincides with that previously obtained by the authors in [2] but with rather more tedious calculations.
Once we have established that the limit problem (3)
does not have a complete system of meromorphic integrals, it follows that
neither does the problem (2) in a neighbourhood
of ![]() .
.
Now, it is enough to apply the usual continuity argument - see [12] or [3] -, since the non-integrability regions correspond to those for which the trace of the monodromy matrices is >2.
However, notice that such an argument is more complicated than simply
checking the aforementioned inequality. In fact, it is necessary to verify
that the Riemann surface, the poles and the loops which are used to calculate
the monodromy matrices do not suffer significant qualitative changes for
any problem close to the limit problem, i.e., in a neighbourhood of ![]() after performing the change of scale. Nevertheless, this can be verified
in an immediate way.
after performing the change of scale. Nevertheless, this can be verified
in an immediate way.
To this end it is enough to realize that the basic solution can be considered
of the form ![]() ,
,
![]() ,
where
,
where ![]() is a solution of the differential equation
is a solution of the differential equation
![]()
which admits as a first integral
![]()
and that the Riemann surface involved in Ziglin's theorem is defined
by the integral
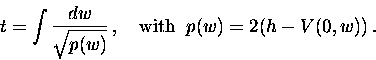
The monodromy group of the normal variation equation is then built by taking closed circuits around the branch points corresponding to the roots of p(w)=0.
In the limit problem, we can take ![]() and n+1 simple poles, roots of wn+1=1,
appear. If the potential is a finite sum of zonal harmonics it is obvious
that the solution
and n+1 simple poles, roots of wn+1=1,
appear. If the potential is a finite sum of zonal harmonics it is obvious
that the solution ![]() still exists and the equation wn+1=1 would
be replaced by another one with the same leading and independent terms
and with lower powers of w multiplied by factors which are positive
powers of
still exists and the equation wn+1=1 would
be replaced by another one with the same leading and independent terms
and with lower powers of w multiplied by factors which are positive
powers of ![]() and hence it goes on having n+1 simple roots provided
and hence it goes on having n+1 simple roots provided ![]() is small enough.
is small enough.
Notice that this result includes as a particular case the non-integrability through meromorphic integrals of the truncated two fixed centres problem in the asymmetric case. The non-integrability of such a problem in the symmetric case was first established by Irigoyen [4] by following a scheme similar to that used for the J2-problem in [3]. We would like to point out that the starting solution used in Irigoyen's work is not suitable for the study of odd harmonics.
On the other hand, although in (1) only the harmonics with negative powers have been included, it is easy to realize that if we add up a finite number of zonal harmonics of the form rkVk to (1), the conclusion still holds. Such terms could be envisaged as coming from the truncation of the development of a perturbation due to a third body by simply assuming some suitable conditions (e.g. the Keplerian orbit is circular and equatorial).