Next: Non-integrability of the Truncated Up: NON-INTEGRABILITY OF THE MOTION Previous: Introduction
![]()
![]()
![]()
Next: Non-integrability
of the Truncated Up: NON-INTEGRABILITY
OF THE MOTION Previous: Introduction
Very broadly speaking, Ziglin's method [14] takes into consideration an analytic Hamiltonian for which a particular solution describing a curve non-homologous to zero on a certain Riemann surface is selected. Then, the non-integrability depends on the properties of the monodromy group associated to the variational equations along such a solution, and particularly on certain non-resonance conditions.
In the case of a Hamiltonian
![]()
where ![]() is homogeneous of an integer degree
is homogeneous of an integer degree ![]() ,
Yoshida [11] obtained very useful criteria,
based on Ziglin's results, by making use of the existence of a straight-line
solution of the form
,
Yoshida [11] obtained very useful criteria,
based on Ziglin's results, by making use of the existence of a straight-line
solution of the form
![]()
where ![]() is a solution of
is a solution of ![]() and
the constant vector
and
the constant vector ![]() is a solution to the algebraic equation
is a solution to the algebraic equation ![]() .
.
In a standard way, the variational equations can be transformed into
a Gauss hypergeometric equation, with well known monodromy group and finally,
the non-integrability depends on the eigenvalues of ![]() ,
one of them always being equal to k-1.
,
one of them always being equal to k-1.
In the planar case, n=2, the problem turns out to be non-integrable
if a coefficient referred to as the integrability coefficient, ![]() ,
lies in certain non-integrability regions Sk ([11];
p. 128, eq. (1.3)), which are derived from the fact that the trace of some
monodromy matrices is >2. For n>2, as shown in [13],
non-integrability follows if the parameters
,
lies in certain non-integrability regions Sk ([11];
p. 128, eq. (1.3)), which are derived from the fact that the trace of some
monodromy matrices is >2. For n>2, as shown in [13],
non-integrability follows if the parameters
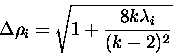
are rationally independent, where the ![]() are the eigenvalues of
are the eigenvalues of ![]() .
.
The reformulation of these criteria into polar or spherical coordinates
presented in [6] has turned out to be useful
in dealing with orbital problems, since it allows us to simplify the calculations,
sometimes very drastically. In the planar case, the integrability coefficient
in polar coordinates is easily computed through
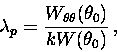
where ![]() is the potential function, k being an integer but
is the potential function, k being an integer but ![]() ,
and
,
and ![]() is a solution to
is a solution to ![]() such that
such that ![]() .
This coefficient relates to Yoshida's integrability coefficient through
the equation
.
This coefficient relates to Yoshida's integrability coefficient through
the equation ![]() .
.