The General Main Satellite Problem

In this section we slightly generalize some results previously obtained by the authors [6] in the sense that we succeed in proving that the (J₂ + J₂₂)-problem is not completely integrable through meromorphic integrals.

Assuming that the primary rotates with constant angular velocity $\omega$ around the Oz axis and using Cartesian coordinates in the rotating system Oxyz attached to the primary, the Hamiltonian is of the form

$$H=\displaystyle\frac{1}{2}(p_x^2+p_y^2+p_z^2)-\omega (xp_y-yp_x)-\displaystyle\frac{\mu}{r}+V_{2}+V_{22}\, ,$$ (4)

with

$$V_2=\displaystyle\frac{\varepsilon _2}{r^3}P_2\left(\displays......dV_{22}=-\displaystyle\frac{\varepsilon _{22}}{r^5}(x^2-y^2)$$

and $\varepsilon _2$, $\varepsilon _{22}$ are constants which are proportional to the small parameters J₂, J₂₂, respectively. Notice that whenever the moments of inertia verify A<B<C, as in the case of the Earth, $\varepsilon _2$ and $\varepsilon _{22}$ are positive.

Since any solution with initial conditions z=p_z=0 always remains in the plane z=0, by making z=p_z=0 in (4), we obtain a new Hamiltonian H₀ whose flow is included in that of (4).

In polar coordinates such a Hamiltonian H₀ is expressed as

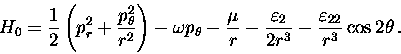$$H_0=\displaystyle\frac{1}{2}\left( p_r^2+ \displaystyle\frac......}-\displaystyle\frac{\varepsilon _{22}}{r^3}\cos 2\theta\, .$$ (5)

It is immediate that if (4) has a first integral which is analytic in z=0, p_z=0 and is independent from H, it will give rise to another first integral which is independent from H₀ for the subproblem (5). On the other hand, if this integral was analytic in $\omega$, at least in $\omega =0$, it would also provide an integral of the auxiliary problem

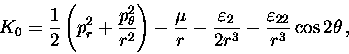$$K_0=\displaystyle\frac{1}{2}\left( p_r^2+ \displaystyle\fra......}-\displaystyle\frac{\varepsilon _{22}}{r^3}\cos 2\theta\, ,$$ (6)

corresponding to a non-rotating primary.

The problem (6) can be treated in a very similar way to that of the zonal harmonics. A suitable change of scale allows us to go to a limit problem, in which the Keplerian term disappears, that is

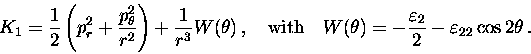$$K_1=\displaystyle\frac{1}{2}\left( p_r^2+ \displaystyle\fra......\frac{\varepsilon _2}{2} -\varepsilon _{22}\cos 2\theta \, .$$ (7)

The integrability coefficient in polar coordinates is extremely easy to calculate. According to what is indicated in section 2, it is enough to consider the solution $\theta _0=0$ to $W_\theta (\theta )=0$. Therefore,

$$\lambda _p=\displaystyle\frac{W_{\theta \theta}(0)}{(-3)W(0)}......varepsilon_{22}}{3(\varepsilon _2/2+\varepsilon _{22})}>0\, .$$

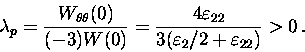
This coefficient lies in one of the non-integrability regions given in [6], so that (7) does not have any additional meromorphic integral.

The usual continuity argument proves that (6) also verifies this property. This allows us to conclude that the original problem (4) does not have any global first integral which is meromorphic and also analytic in w=0, and in z=p_z=0. This result generalizes those previously obtained by the authors ([2], [6]), where only the non-existence of additional rational integrals was proved, either for the case $\varepsilon _2 = 0$ or for the general case.