Siguiente: Relaciones de equivalencia Subir: Relaciones binarias en un Anterior: Relaciones binarias en un   Índice General

Propiedades de las relaciones binarias

De entre las diversas propiedades que puede (o no) tener una relación binaria en $A$, las más interesantes son las siguientes:

1. Reflexiva: si $x R x$, $\forall x\in A$.
2. Irreflexiva: si $x R\!\!\!\!/\;x$, $\forall x\in A$.
3. Simétrica: si $\forall x,y\in A$, $x R y\Rightarrow y R x$.
4. Antisimétrica: si $\forall x,y\in A$, $(x R y)\wedge(y R x)\Rightarrow x=y$.
5. Transitiva: si $\forall x,y,z\in A$, $(x R y)\wedge(y R z)\Rightarrow(x R z)$.
6. Intransitiva: si $\forall x,y,z\in A$, $(x R y)\wedge(y R z)\Rightarrow(x R\!\!\!\!/\;z)$.

Hacemos notar que las propiedades anteriores son comprobables a partir de la matriz de la relación $R$, siempre (por supuesto) que el conjunto $A$ sea finito. Para ello, necesitamos previamente un poco más de terminología. Así se denomina relación diagonal en $A$, y se denota por $\Delta$, a la relación definida por

$$\Delta:=\{(x,x)\in A\times A\;\vert\;x\in A\}$$

Obviamente, la matriz asociada a la relación diagonal es aquélla que tiene 1 en todas las posiciones de la diagonal y 0 en el resto, matriz que denominaremos identidad y representaremos por $I$. De esta manera, se obtiene fácilmente el siguiente

Teorema 4.1   Sea $R\subseteq A\times A$ y sea $M$ la matriz asociada a $R$. Entonces:

1. $\mbox{$R$ es reflexiva}$$\Leftrightarrow (\Delta\subseteq R) \Leftrightarrow (I\Rightarrow M)$, es decir, si $M$ tiene 1 en todas las posiciones de la diagonal.
2. $\mbox{$R$ es irreflexiva}$$\Leftrightarrow (\Delta\cap R=\emptyset) \Leftrightarrow (M\Rightarrow\neg I)$, es decir, si $M$ tiene 0 en todas las posiciones de la diagonal.
3. $\mbox{$R$ es simétrica}$$\Leftrightarrow (R=R^{-1}) \Leftrightarrow (M=M^{t})$, es decir, si $M$ es simétrica.
4. $\mbox{$R$ es antisimétrica}$$\Leftrightarrow (R\cap R^{-1}\subseteq\Delta) \Leftrightarrow (M\ast M^{t}\Rightarrow I)$, es decir, si no existen fuera de la diagonal $(i\neq j)$ dos posiciones simétricas cuyos valores sean 1 simultáneamente.
5. $\mbox{$R$ es transitiva}$$\Leftrightarrow (R\circ R\subseteq R) \Leftrightarrow (M\cdot M\Rightarrow M)$.
6. $\mbox{$R$ es intransitiva}$$\Leftrightarrow (R\circ R\subseteq \overline{R}) \Leftrightarrow (M\cdot M\Rightarrow\neg M)$.

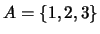
Ejemplo 4.2   Sobre el conjunto $A=\{1,2,3\}$ se considera la relación

$$R=\{(1,3),(2,3),(3,2)\}$$

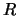
Es evidente a simple vista que $R$ no es transitiva, pero lo podemos comprobar mediante la matriz asociada

$$M=\left[\begin{array}{ccc} 0&0&1\\ 0&0&1\\ 0&1&0\end{array}\right]$$

Efectivamente

$$M\cdot M= \left[\begin{array}{ccc} 0&0&1\\ 0&0&1\\ 0&1&0\en... ...ht] = \left[\begin{array}{ccc} 0&1&0\\ 0&1&0\\ 0&0&1\end{array}\right]$$

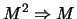
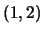
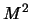
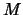
y se ve fácilmente que la implicación $M^{2}\Rightarrow M$ es falsa (por ejemplo) en la posición $(1,2)$, donde en $M^{2}$ hay 1 y en $M$ hay 0.

Siguiente: Relaciones de equivalencia Subir: Relaciones binarias en un Anterior: Relaciones binarias en un   Índice General