Siguiente: Retículo Subir: Estructuras algebraicas Anterior: Anillo
Un anillo
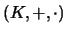 es un cuerpo si verifica la condición adicional de que
es un cuerpo si verifica la condición adicional de que
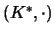 sea un grupo, donde
sea un grupo, donde
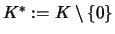 . Es decir
Si además el producto es conmutativo, se trata de un cuerpo conmutativo.
. Es decir
Si además el producto es conmutativo, se trata de un cuerpo conmutativo.
Ejemplo 2.4

- Los conjuntos
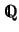 ,
IR y
,
IR y
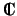 son cuerpos con sus sumas y productos
respectivos.
son cuerpos con sus sumas y productos
respectivos.
- Si
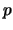 es un número primo (positivo) y
es un número primo (positivo) y
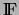
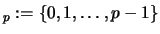 ,
y las sumas y productos se realizan `` módulo
,
y las sumas y productos se realizan `` módulo 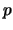 '', entonces
'', entonces
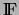
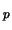 es un cuerpo (finito).
es un cuerpo (finito).
- Si se quiere construir un cuerpo no conmutativo, hace falta recurrir a
los llamados `` cuaterniones''. Se dejan los detalles como ejercicio
(avanzado). Se considera el conjunto (de cuaterniones) dado por
IK
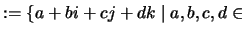
IR
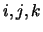 son variables que verifican las siguientes relaciones
y donde la suma y el producto se realizan como si fueran polinomios, con las
simplificaciones derivadas de las reglas anteriores.
son variables que verifican las siguientes relaciones
y donde la suma y el producto se realizan como si fueran polinomios, con las
simplificaciones derivadas de las reglas anteriores.
Jose Ignacio Farran Martin
2003-07-16