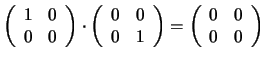Siguiente: Cuerpo Subir: Estructuras algebraicas Anterior: Grupo
Un anillo es una terna
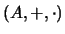 tal que:
tal que:
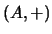 es un grupo abeliano.
es un grupo abeliano.
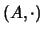 es un semigrupo.
es un semigrupo.
- El producto es distributivo respecto de la suma.
Si además existe elemento neutro 1 (o unidad) del producto, el anillo
se dice unitario, y si el producto es conmutativo se trata de un
anillo conmutativo (puede ser ambas cosas, que es el caso más corriente,
y entonces se trata de un anillo conmutativo y unitario).
Ejemplo 2.3

-
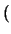 Z Z
Z Z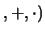 es un anillo conmutativo y unitario.
es un anillo conmutativo y unitario.
- Si
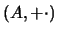 es un anillo conmutativo (y unitario) entonces
los polinomios en un número finito de indeterminadas con coeficientes en
es un anillo conmutativo (y unitario) entonces
los polinomios en un número finito de indeterminadas con coeficientes en 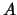 ,
junto con la suma y el producto usuales, es decir,
,
junto con la suma y el producto usuales, es decir,
![$ (A[X_{1},\ldots,X_{n}],+,\cdot)$](img52.png) es un anillo conmutativo (y unitario).
es un anillo conmutativo (y unitario).
- Las matrices cuadradas
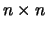 con la suma y el producto de matrices
forman un anillo unitario (no conmutativo).
con la suma y el producto de matrices
forman un anillo unitario (no conmutativo).
-
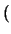 IN
IN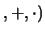 es lo que se denomina un semianillo conmutativo y unitario;
se deja como ejercicio escribir las definiciones adecuadas.
es lo que se denomina un semianillo conmutativo y unitario;
se deja como ejercicio escribir las definiciones adecuadas.
Por otra parte, se dice que
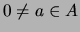 es un divisor de cero si
existe
es un divisor de cero si
existe
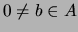 tal que
tal que
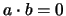 (por tanto,
(por tanto, 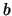 también lo es).
Por ejemplo, en el anillo de matrices
también lo es).
Por ejemplo, en el anillo de matrices 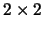 de coeficientes reales
con la suma y el producto usuales se tiene que
con lo que ambas matrices son divisores de cero. Así pues,
si en un anillo no existen divisores de cero, es decir
entonces se dice que el
de coeficientes reales
con la suma y el producto usuales se tiene que
con lo que ambas matrices son divisores de cero. Así pues,
si en un anillo no existen divisores de cero, es decir
entonces se dice que el 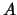 es un anillo íntegro o dominio de integridad
(abreviadamente se suele decir que
es un anillo íntegro o dominio de integridad
(abreviadamente se suele decir que 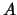 es un dominio).
Por lo que acabamos de ver, las matrices cuadradas no constituyen un
dominio de integridad. En cambio, el anillo de enteros es íntegro,
así como los anillos de polinomios con coeficientes en un dominio
(por ejemplo
Z Z
es un dominio).
Por lo que acabamos de ver, las matrices cuadradas no constituyen un
dominio de integridad. En cambio, el anillo de enteros es íntegro,
así como los anillos de polinomios con coeficientes en un dominio
(por ejemplo
Z Z![$ [X_{1},\ldots,X_{n}]$](img60.png) ).
).
Siguiente: Cuerpo Subir: Estructuras algebraicas Anterior: Grupo
Jose Ignacio Farran Martin
2003-07-16