Siguiente: Anillo Subir: Estructuras algebraicas Anterior: Semigrupo
Un grupo es un monoide 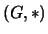 en el que todo elemento
en el que todo elemento 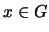 tiene inverso.
Si además se verifica la propiedad conmutativa, se dice que el grupo es abeliano
(o conmutativo). En la práctica, cuando un grupo es abeliano la operación se
denota en forma de suma, y en caso contrario se denota en forma de producto.
En el primer caso (notación aditiva), el elemento neutro se denota por 0 (cero)
y el elemento `` opuesto'' de
tiene inverso.
Si además se verifica la propiedad conmutativa, se dice que el grupo es abeliano
(o conmutativo). En la práctica, cuando un grupo es abeliano la operación se
denota en forma de suma, y en caso contrario se denota en forma de producto.
En el primer caso (notación aditiva), el elemento neutro se denota por 0 (cero)
y el elemento `` opuesto'' de 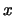 se denota por
se denota por 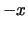 , y en el segundo
caso (notación multiplicativa), el elemento neutro se denota por
, y en el segundo
caso (notación multiplicativa), el elemento neutro se denota por 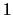 (unidad)
y el elemento `` inverso'' de
(unidad)
y el elemento `` inverso'' de 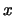 se denota por
se denota por 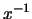 .
.
Siguiente: Anillo Subir: Estructuras algebraicas Anterior: Semigrupo
Jose Ignacio Farran Martin
2003-07-16
 Z Z
Z Z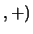 como
como
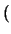 IR
IR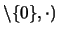 son grupos abelianos.
son grupos abelianos.
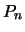 de `` permutaciones''
de
de `` permutaciones''
de 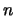 elementos
elementos
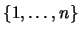 , junto con la operación
de composición, es un grupo no conmutativo,
entendiendo una permutación como una aplicación biyectiva
, junto con la operación
de composición, es un grupo no conmutativo,
entendiendo una permutación como una aplicación biyectiva
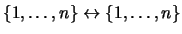
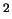 (o en
IR
(o en
IR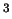 )
con la composición también son un grupo no conmutativo, entendiendo por
movimiento rígido un tipo especial de aplicaciones biyectivas
(aquellas que conservan distancias y ángulos, es decir, esencialmente simetrías, giros y traslaciones).
)
con la composición también son un grupo no conmutativo, entendiendo por
movimiento rígido un tipo especial de aplicaciones biyectivas
(aquellas que conservan distancias y ángulos, es decir, esencialmente simetrías, giros y traslaciones).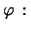 IR
IR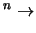 IR
IR
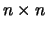 son un grupo abeliano
para la suma, mientras que las matrices cuadradas inversibles (con
determinante no nulo) son un grupo no conmutativo para el producto.
son un grupo abeliano
para la suma, mientras que las matrices cuadradas inversibles (con
determinante no nulo) son un grupo no conmutativo para el producto.