Siguiente: Grupo Subir: Estructuras algebraicas Anterior: Estructuras algebraicas
Un semigrupo es un par 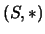 donde `
donde `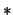 ' es una operación interna
en
' es una operación interna
en 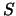 que verifica la propiedad asociativa. Es por tanto la estructura algebraica
más sencilla posible. Si además la operación tiene elemento neutro en
que verifica la propiedad asociativa. Es por tanto la estructura algebraica
más sencilla posible. Si además la operación tiene elemento neutro en 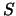 , se dice
que
, se dice
que 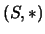 es un monoide. En cualquiera de los dos casos (semigrupo o monoide),
si se verifica además la propiedad conmutativa, se dice que el semigrupo (o el
monoide) es conmutativo o abeliano.
es un monoide. En cualquiera de los dos casos (semigrupo o monoide),
si se verifica además la propiedad conmutativa, se dice que el semigrupo (o el
monoide) es conmutativo o abeliano.
Ejemplo 2.1

- Tanto
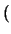 IN
IN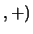 como
como
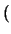 IN
IN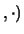 son monoides conmutativos.
son monoides conmutativos.
- Dado un alfabeto de símbolos
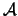 , el conjunto de
cadenas de símbolos junto con la operación de concatenar cadenas sin
cancelaciones entre símbolos es un semigrupo no conmutativo (o un
monoide no conmutativo, si se considera la palabra vacía como posible).
Esta estructura se utiliza en la Teoría de Lenguajes Formales.
, el conjunto de
cadenas de símbolos junto con la operación de concatenar cadenas sin
cancelaciones entre símbolos es un semigrupo no conmutativo (o un
monoide no conmutativo, si se considera la palabra vacía como posible).
Esta estructura se utiliza en la Teoría de Lenguajes Formales.
Jose Ignacio Farran Martin
2003-07-16
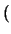 IN
IN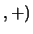 como
como
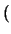 IN
IN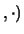 son monoides conmutativos.
son monoides conmutativos.
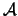 , el conjunto de
cadenas de símbolos junto con la operación de concatenar cadenas sin
cancelaciones entre símbolos es un semigrupo no conmutativo (o un
monoide no conmutativo, si se considera la palabra vacía como posible).
Esta estructura se utiliza en la Teoría de Lenguajes Formales.
, el conjunto de
cadenas de símbolos junto con la operación de concatenar cadenas sin
cancelaciones entre símbolos es un semigrupo no conmutativo (o un
monoide no conmutativo, si se considera la palabra vacía como posible).
Esta estructura se utiliza en la Teoría de Lenguajes Formales.