



Cálculos correspondientes al apartado 1)
La superficie S que debemos considerar es una superficie esférica de radio
R=6.380 Km. ya que el problema parte de la suposición de que la Tierra
es esférica.
El sistema de coordenadas esféricas permite obtener una parámetrización de S donde los parámetros son precisamente los ángulos que dan la latitud y la longitud de cada punto medidas como indica el problema.
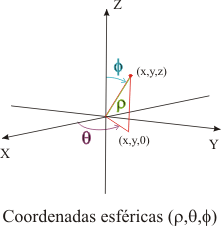
La relación entre las coordenadas cartesianas y las esféricas es
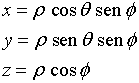
La ecuación de una esfera en el último sistema es ρ=cte. En nuestro caso ρ=R=6.380.
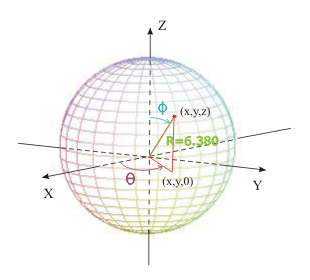
La parametrización de S será:
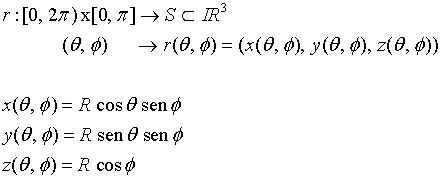
Los coeficientes de la primera forma fundamental permiten
calcular el área de una porción de la superficie S mediante la fórmula
![]()
donde D es el dominio de variación de los parámetros para dicha porción de superficie.
Calculamos los primeros coeficientes fundamentales E, F y G:
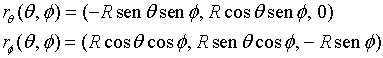
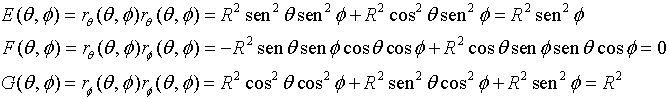
El dominio D de variación de los parámetros es el rectángulo que aparece en el siguiente dibujo
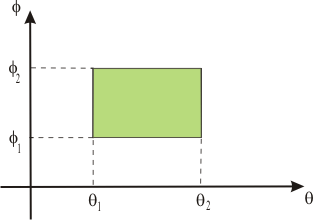
Sustituyendo en la fórmula y haciendo los cálculos pertinentes
se obtiene
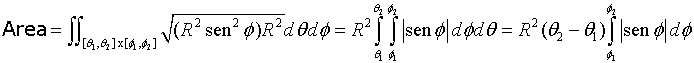
Como el ángulo Φ varia en [0,π] su seno será siempre positivo y calculando la última integral tendremos
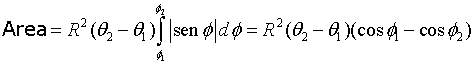
Volver a página de instrucciones