Cálculos correspondientes al apartado 4)
El trabajo realizado por una fuerza a lo largo de una trayectoria C viene dado por su integral de línea
En nuestro caso la fuerza está dada por el campo vectorial 
que tiene la ventaja de ser irrotacional como se comprueba haciendo el cálculo
correspondiente:
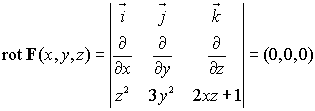
Esto significa que F es un campo conservativo y por lo tanto tiene una función potencial asociada que denotamos por f y la integral de línea se puede calcular mediante la fórmula (de Barrow generalizada)
donde los puntos (x0,y0,z0) y (x1,y1,z1) son los extremos inicial y final de la trayectoria, respectivamente.
Cálculo de la función potencial
Calculamos el potencial de F
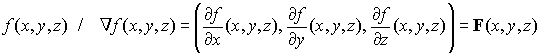
de donde se obtienen las igualdades siguientes
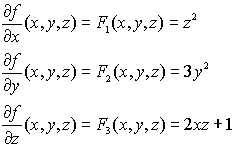
Integrando respecto de x en la primera ecuación:
Para obtener k(y,z) integramos las otras dos ecuaciones, la segunda respecto de y:
y la tercera respecto de z
La función potencial es
Finalmente el trabajo será
Es posible calcular el trabajo hallando directamente la integral de línea utilizando la parametrización de C, σ(θ), conseguida en el apartado 1):
Pero en este caso los cálculos son bastante más largos.
Volver a página de instrucciones