



Enunciado del Problema
Un ciclista sube una montaña siguiendo una ruta que da una vuelta alrededor de la misma, partiendo de un punto en la base y llegando a la cima. Matemáticamente la superficie de la montaña, convenientemente escalada, responde a la ecuación
![]()
La proyección sobre el plano XY de la trayectoria seguida por el ciclista en su ascenso es un tramo de espiral de Arquímedes cuya ecuación en coordenadas polares es
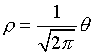
- Dése una parametrización de la superficie y obténgase una representación paramétrica regular de la curva seguida por el ciclista en su ascenso. Calcúlense los extremos de esta curva.
- Para la parametrización de la montaña dada en el apartado anterior, estúdiese la regularidad y calcúlese la primera forma fundamental.
- Utilizando la regla de Simpson compuesta de 4 intervalos, obténgase una estimación de la distancia recorrida en el ascenso por el ciclista.
- Durante el ascenso, la resultante de las fuerzas que actúan sobre el ciclista viene descrita por el campo vectorial
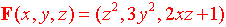
¿Cuál es el trabajo realizado por la fuerza F en el ascenso a la montaña desde su base hasta su cima?
La lluvia azota la montaña por su cara sur con un campo de velocidad dado por
Calcúlese el flujo de F a través de la superficie de la cara sur de la montaña (tómese como tal la zona con
).