



Cálculos correspondientes al apartado 2)
Estudio de la regularidad
Para estudiar la regularidad de la parametrización dada para la superficie
en el apartado 1) calculamos las derivadas parciales de r
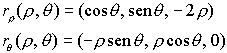
En cada punto su producto vectorial da un vector normal a la superficie:
![]()
En los puntos en los que este vector no este definido o sea cero la superficie parametrizada no será regular. En nuestro caso el vector normal está siempre definido; veamos si se anula para algún valor de los parametros. Para ello estudiamos el cuadrado de su módulo
![]()
El segundo factor no se anula para ningún valor de ρ, pero el primero si lo hace cuando ρ=0, luego
![]()
y por lo tanto la parametrización no es regular en los puntos de la forma r(0, θ). Realmente la imagen de (0, θ) es un único punto sobre la superficie: el que da la cima de la montaña (0,0, 2π).
Primera forma fundamental
Para obtener la primera forma fundamental, calculamos los primeros coeficientes fundamentales E, F y G
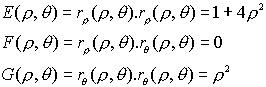
La primera forma fundamental queda:
![]()
Volver a página de instrucciones