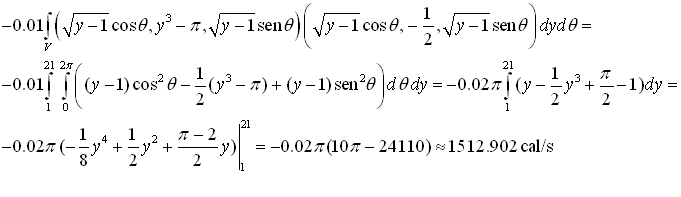Cálculos correspondientes al apartado 5)
El flujo de calor a través de una superficie S asociado a una distribución de temperatura T(x,y,z) viene dado por
![]()
donde k es una constante que representa la conductividad térmica y
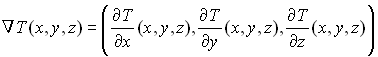
es el vector gradiente del campo escalar T.
En nuestro caso la distribución de temperatura viene dada por la función
![]()
Derivando obtenemos
![]()
El flujo de calor a través de S será
![]()
Según la definición de integral de superficie para un campo vectorial
![]()
donde se ha considerado para la superficie del faro la parametrización r dada en el problema. Sustituyendo y teniendo en cuenta que los parámetros varían en V=[1,21]x[0,2π], calculamos el flujo: