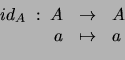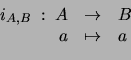Aplicaciones: conceptos generales

Definición 1.1 $\;$

Sean 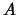y 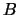dos conjuntos; se llama correspondencia (o relación) de 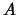en 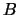, y se denota

$\displaystyle f\;:\;A\rightarrow B$
a cualquier terna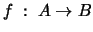

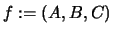
$\displaystyle f:=(A,B,C)$
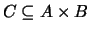donde $C\subseteq A\times B$ .
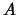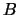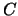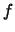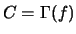se llama conjunto inicial, se llama conjunto final, y se llama `` grafo'' de la correspondencia , y se denota $C=\Gamma(f)$ .
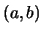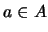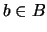Si un par , donde $a\in A$ y $b\in B$ , está en el grafo de 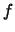, se denota 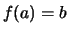(o bien 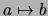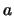$a\mapsto b$ ), se dice que es origen (o preimagen) de 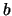, y 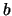se dice que es imagen de .
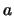Dos correspondencias 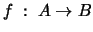y 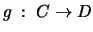son iguales si y sólo si suceden tres cosas:
3. $\Gamma(f)=\Gamma(g)$

Definición 1.2 $\;$

Se llama dominio de la correspondencia $f\;:\;A\rightarrow B$ al conjunto

$\displaystyle Dom(f):=\{a\in A\;\vert\;f(a)=b,\;\exists b\in B\}\subseteq A$
Se llama imagen (también codominio, rango o recorrido) de la correspondencia $f\;:\;A\rightarrow B$ al conjunto

$\displaystyle Im(f):=\{b\in B\;\vert\;f(a)=b,\;\exists a\in A\}\subseteq B$

Definición 1.3 Una correspondencia $f\;:\;A\rightarrow B$ se dice que es una `` aplicación'' (o función) si

$\displaystyle \forall a\in A,\;\exists_{1} b\in B\;\;\vert\;\; f(a)=b$

es decir

(Todo elemento de

tiene una única imagen).

Definición 1.4 $\;$

Una aplicación $f\;:\;A\rightarrow B$ es inyectiva si

$\displaystyle f(a)=f(b)\Rightarrow a=b$
(Elementos distintos tienen imágenes distintas).
Una aplicación $f\;:\;A\rightarrow B$ es suprayectiva (sobreyectiva o sobre) si

$\displaystyle \forall b\in B\;\;\exists a\in A\;\;,\;\;\;\;f(a)=b$
es decir

$\displaystyle Im(f)=B$
(Todos los elementos de son imágenes).
Una aplicación $f\;:\;A\rightarrow B$ es biyectiva si es a la vez inyectiva y suprayectiva.

Ejemplo 1.5 $\;$

La aplicación identidad en un conjunto dada por

$\begin{displaymath} \begin{array}{rcl} id_{A}\;:\;A&\rightarrow&A\\ a&\mapsto&a \end{array} \end{displaymath}$
es una biyección.
Dada una contención de conjuntos $A\subseteq B$ se tiene una `` inyección canónica''

$\begin{displaymath} \begin{array}{rcl} i_{A,B}\;:\;A&\rightarrow&B\\ a&\mapsto&a \end{array} \end{displaymath}$

Definición 1.6 Sea una aplicación $f\;:\;A\rightarrow B$ .

Se llama imagen directa de $C\subseteq A$ por al conjunto

$\displaystyle f(C):=\{f(c)\;\vert\;c\in C\}$
Se llama imagen inversa (o recíproca) de $C\subseteq B$ por al conjunto

$\displaystyle f^{-1}(C):=\{a\in A\;\vert\;f(a)\in C\}$
En el caso particular de que $C=\{b\}$ tenga un solo punto, se denota

$\displaystyle f^{-1}(b)\equiv f^{-1}(\{b\})$

Teorema 1.7 Sean $f\;:\;A\rightarrow B$ , $A_{1},A_{2}\subseteq A$ y $B_{1},B_{2}\subseteq B$ .

$f(A_{1}\cup A_{2})=f(A_{1})\cup f(A_{2})$ .
$f(A_{1}\cap A_{2})\subseteq f(A_{1})\cap f(A_{2})$ , y se da la igualdad si es inyectiva.
Si $A_{1}\subseteq A_{2}$ entonces $f(A_{1})\subseteq f(A_{2})$ .
$f^{-1}(B_{1}\cap B_{2})=f^{-1}(B_{1})\cap f^{-1}(B_{2})$ .
$f^{-1}(B_{1}\cup B_{2})=f^{-1}(B_{1})\cup f^{-1}(B_{2})$ .
Si $B_{1}\subseteq B_{2}$ entonces $f^{-1}(B_{1})\subseteq f^{-1}(B_{2})$ .
$f^{-1}(B\setminus B_{1})=A\setminus f^{-1}(B_{1})$ .
(La imagen inversa del complementario es el complementario de la imagen inversa).
$A_{1}\subseteq f^{-1}(f(A_{1}))$ , y se da la igualdad si es inyectiva.
$f(f^{-1}(B_{1}))\subseteq B_{1}$ , y se da la igualdad si es suprayectiva.