3. Problems with the 2. Identification penalties 2.2 Linear orbit identification

2.3 Restricted orbit identification

For the reasons discussed in Section 3, it is not always possible to use the linear identification theory based upon all 6 orbital elements. The question is how to use the same algorithm on a subset of the orbital elements? The answer is implicit in the arguments presented in [Paper I], Section 2.3, Case 2, which we are going to use without repeating the formal proofs.

Let us suppose that the vector of estimated parameters is split into two components, along linear subspaces of the parameter space:

$$X=\pmatrix{L \cr E}\ ,$$

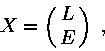
where $E$ are elements of interest. The normal and covariance matrices $C$ and $\Gamma$ are decomposed as follows:

$$C=\pmatrix{C_L & C_{LE}\cr C_{EL}&C_E}\, ,\qquad\pmatrix{\Gamma_L & \Gamma_{LE}\cr \Gamma_{EL}&\Gamma_E}$$

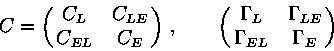
Then the uncertainty of $E$ for arbitrary $L$ can be described by the penalty, with respect to the minimum point $E^*$

$$\Delta Q \simeq {\displaystyle 2 \over \displaystyle m} \, (E......t C^E\, (E-E^*)\, ,\qquad C^E= C_E -C_{EL}\,C_L^{-1}\, C_{LE}$$

and by the marginal covariance matrix $\Gamma_E=\left(C^E\right)^{-1}$.

Note that the marginal normal matrix $C^E$ is not $C_E$ and that to obtain the penalty of the above formula as a function of $E$, the value of $L$ has to be changed with respect to the nominal solution $L^*$ of the unrestricted problem, by an amount which is a function of $E$:

$$L-L^*= -C_L^{-1}C_{LE}\,(E-E^*)\ .$$

Let us apply this restricted penalty formula to the restricted identification problem. Let $(L_1,E_1)$ and $(L_2,E_2)$ be the nominal solutions for the two arcs considered separately, and $C^E_1$ and $C^E_2$ the corresponding marginal normal matrices. The variables $L$ are given as function of $E$ by:

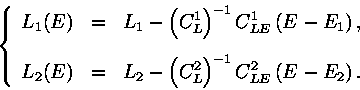$$\left\{\begin{array}{lcr}{\displaystyle L_1(E)} & {\display......eft(C^2_L\right)^{-1}C^2_{LE}\,(E-E_2)\, .}\end{array}\right.$$ (3)

By the same formalism of the previous subsection:

$${\displaystyle m \over \displaystyle 2} \, \Delta Q \simeq (E-E_0)\cdot C^E_0\, (E-E_0) + K_E$$

with

$$C^E_0=C^E_1+C^E_2$$

$$E_0=\left(C^E_0\right)^{-1}\,\left(C^E_1E_1 + C^E_2 E_2\right)$$

$$K_E=\Delta E \cdot C^E \, \Delta E$$

$$C^E=C^E_2-C^E_2\left(C^E_0\right)^{-1}C^E_2=C^E_1-C^E_1\left(C^E_0\right)^{-1}C^E_1\ .$$

Note that $K_E$ is not the same as the complete minimum penalty $K$ of the previous section. The estimate $K_E$ of the minimum penalty is obtained by assuming that $L=L_1(E)$ in the computation of $\DeltaQ_1$ while $L=L_2(E)$ in the computation of $\Delta Q_2$. Thus there is, in general, no complete solution with a single $X=(L,E)$ to be fit to the observations of both arcs with penalty $K_E$, but such value is obtained by using $(L_1(E_0), E_0)$ in the first arc, $(L_2(E_0), E_0)$ in the second arc, $E_0$ being the proposed restricted identification.

We claim that $K_E\leq K$: $K_E$ is the minimum of the penalty over the space of variables $(E,L_1, L_2)$, while $K$ is the minimum of the same penalty over the same space but with the additional constraint $L_1=L_2$, and the minimum of a function can only increase when constraints are added.

In conclusion, the proposed restricted identification $E_0$ is not a complete identification, and the corresponding minimum penalty $K_E$ is not the full penalty to be paid to achieve a full identification. This procedure is, however, a good way to filter the possible identifications because $K_E\leq K$: if a couple can be discarded as a possible identification with the restricted computation, because $K_E$ is too large, then it does not need to be tested with the complete algorithm.

Note that it is also possible to define a constrained identification algorithm, based upon the conditional covariance matrices and the algorithm for constrained optimisation on linear subspaces, as outlined in [Paper I], Section 2.3.

3. Problems with the 2. Identification penalties 2.2 Linear orbit identification