Next: 2.3 Restricted orbit identification Up: 2. Identification penalties Previous: 2.1 Differential corrections as
![]()
![]()
![]()
Next: 2.3
Restricted orbit identification Up: 2.
Identification penalties Previous: 2.1
Differential corrections as
By orbit identification problem we mean to find an algorithm
to determine which couples of orbits, among many included in some catalog,
might belong to the same object. We assume that both orbits, for which
the possibility of identification is being investigated, have been obtained
as solutions of a least squares problem. Note that this is not always the
case for orbit catalogs containing asteroids observed only over a short
arc. There are therefore two uniquely defined vectors of elements, ![]() and
and ![]() ,
and the normal and covariance matrices
,
and the normal and covariance matrices ![]() computed after convergence of the iterative differential correction procedure,
that is at
computed after convergence of the iterative differential correction procedure,
that is at ![]() .
The two target functions of the two separate orbit determination processes
are:
.
The two target functions of the two separate orbit determination processes
are:
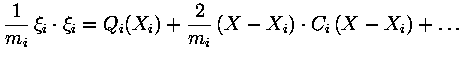 |
|||
|
|
where ![]() are the two vectors of dimensions
are the two vectors of dimensions ![]() of residuals of the separate orbit determination processes.
of residuals of the separate orbit determination processes.
For the two orbits to represent the same object, observed at different
times, we need to find a low enough minimum for the joint target function,
formed with the sum of squares of the ![]() residuals:
residuals:
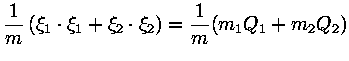 |
|||
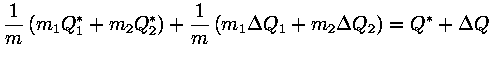 |
where ![]() is the value corresponding to the sum (with suitable weighting) of the
two separate minima, and the penalty
is the value corresponding to the sum (with suitable weighting) of the
two separate minima, and the penalty ![]() measures the increase in the target function which results from the need
to use the same orbit for both sets of observations.
measures the increase in the target function which results from the need
to use the same orbit for both sets of observations.
The linear algorithm to solve the problem is obtained when the quasi-linear
approximation can be used, not only locally, in the neighborhood of the
two separate solutions ![]() and
and ![]() ,
but even globally for the joint solution. This is a very strong assumption,
because in general we cannot assume that the two separate solutions are
near to each other, but if the assumption is true, we can use the quadratic
approximation for both penalties
,
but even globally for the joint solution. This is a very strong assumption,
because in general we cannot assume that the two separate solutions are
near to each other, but if the assumption is true, we can use the quadratic
approximation for both penalties ![]() ,
and obtain an explicit formula for the solution of the identification problem:
,
and obtain an explicit formula for the solution of the identification problem:
![]()
![]()
Neglecting higher order terms, the minimum of the penalty ![]() can be found by minimizing the nonhomogeneous quadratic form of the formula
above. If the new joint minimum is
can be found by minimizing the nonhomogeneous quadratic form of the formula
above. If the new joint minimum is ![]() ,
then by expanding around
,
then by expanding around ![]() we have
we have
![]()
and by comparing the last two formulas we find:
If the matrix ![]() ,
which is the sum of the two separate normal matrices
,
which is the sum of the two separate normal matrices ![]() and
and ![]() ,
is positive-definite, then it is invertible and we can solve for the new
minimum point:
,
is positive-definite, then it is invertible and we can solve for the new
minimum point:
![]()
This equation has a very simple interpretation in terms of the differential
correction process: at convergence in each one of the two separate pseudo-Newton
iterations, ![]() with
with ![]() and
and ![]() ;
therefore
;
therefore
![]()
The assumption that the quasi-linear approach is applicable to the identification
means that ![]() can be kept constant, thus they have the same value at
can be kept constant, thus they have the same value at ![]() and at
and at ![]() ;
under these conditions
;
under these conditions ![]() can be interpreted as the result of the first differential correction iteration
for the joint problem.
can be interpreted as the result of the first differential correction iteration
for the joint problem.
The computation of the minimum identification penalty ![]() can be simplified by taking into account that
can be simplified by taking into account that ![]() is translation invariant:
is translation invariant:
![]()
![]()
Then we can compute ![]() after a translation by
after a translation by ![]() ,
that is assuming
,
that is assuming ![]() ,
,
![]() ,
and
,
and ![]() :
:
![]()
and by defining
![]()
we have a simple expression of ![]() as a quadratic form:
as a quadratic form:
![]()
Alternatively, translating by ![]() ,
that is with
,
that is with ![]() ,
,
![]() and
and ![]() :
:
![]()
and the same matrix ![]() can be defined by the alternative expression:
can be defined by the alternative expression:
![]()
Note that both these formulas only assume that ![]() exists. Under this hypothesis
exists. Under this hypothesis
| |
(2) |
This is true in exact arithmetic, but might be difficult to realize
in a numerical computation if the matrix ![]() is badly conditioned.
is badly conditioned.
We can summarize the conclusions by the formula
![]()
which gives the minimum identification penalty ![]() and also allows one to assess the uncertainty of the identified solution,
by defining a confidence ellipsoid with matrix
and also allows one to assess the uncertainty of the identified solution,
by defining a confidence ellipsoid with matrix ![]() .
.