6. Conclusions and future THE ASTEROID IDENTIFICATION PROBLEM 4.1 Test on 100

5. New Identifications

After a more than six year hiatus the global dataset of astrometric observations of asteroids was recently made available to the scientific community, permitting us to test the theory described in this paper. In this section we outline our procedure to find new orbit identifications starting from this dataset, and the results we have obtained.

We have used the dataset available (by subscription only) from the Minor Planet Center (MPC), containing all the published asteroid observations. This dataset is currently updated near each full moon, and we have used the March 2, 1999 and the April 2, 1999 updates in our testing. In the following discussion all numbers refer to the April catalog unless stated otherwise.

To give an idea of the size of the archive of observations, consider that the dataset for only the unnumbered asteroids contains $1\,157\,884$ observations for $121\,090$ designations. This does not imply that there are really more than $100\,000$ distinct asteroids which have been observed, but only that there have been that many separate discoveries. In fact, there are $15\,461$ (secondary) designations belonging to objects that have been identified with $11\,231$ other (primary) designations. Note that these identifications do not necessarily lead to multi-opposition orbits, because sometimes two sets of observations belonging to the same opposition/apparition are identified (the MPC uses the specific term double designations for these cases). These numbers of identifications refer to the April situation, thus they already include identifications that we had ourselves proposed in March, and which had already been processed by the MPC. There are $94\,398$ designations that have never been identified with another.

The first step is to compute a catalog of orbits, complete with normal and covariance matrices, but it is neither possible nor useful to compute orbits for each one of the $94\,398+11\,231$ ``asteroids'' in the files. There are $8\,367$ identifiers corresponding to a single observation, and these are essentially useless. There are also $8\,870$ identifiers corresponding to two observations, and some of these can be used for attributions, as we will discuss in a later paper in this series; however, they cannot be used to compute a full orbit with six independently solved for orbital elements. There are another $31\,946$ identifiers corresponding to at least $3$observations, which, however, span less than $4$ days; for many of these an orbit could be computed, but it would be very poorly constrained. All the difficulties described in Section 3 would be very severe for such very short arc orbits, and methods more suitable to strongly nonlinear identifications are necessary. An additional difficulty arises from observations which have been reported only as rough positions; an arc including less than 3 `good' observations might result in a nominal orbit, which is however of little significance. Finally, no quality control can be performed on arcs containing only the minimum number of 3 observations, and residual normalization is meaningless.

For these reasons we have selected only the $35\,857$ objects for which there are at least 4 `good' observations, and with arcs of at least 4 days. Of these, there were $737$ objects for which we could not compute an unconstrained orbit with our automated orbit determination software. So we have computed $11\, 875$ orbits with observed arcs longer than $180$ days, $11\,399$ orbits with arcs between $20$ and $180$ days, and $11\,846$ orbits with arcs between $4$ and $20$ days. We have thus assembled a catalog with $35\,121$ orbits (including (719) Albert, the only lost numbered asteroid). Each of these orbits has been computed as the solution of a least squares fit with convergent differential corrections. The automated outlier rejection used in this process will be described in another paper of this series, but in practice the control parameters were such that the outlier removal was inactive for short arcs, and quite effective for multi-opposition orbits. The residual normalization was applied by using the maximum between $1$ arc-sec and the actual residuals RMS. Thus normal and covariance matrices were available for each orbit.

To minimize the effect of nonlinearity in the propagation of the confidence regions, we have implemented a method whereby we can access different catalogs at several different epochs, in order to use for each couple being tested the epoch closest to the midpoint of the two central epochs. This results in a measurable, but not dramatic (about $10\%$), increase of the number of real identifications found.

To apply the algorithm described in Sections 2 and 4, we have to perform $35\,121\times 35\,120/2$ computations of the orbit plane distance $d_2$; $3\,895\,552$ couples passed the test $d_2<30$, for these the distance $d_5$ (based upon all elements but $\lambda$) was computed, and $300\,977$ passed the test $d_5<5\,000$. For the latter, the full linear identification distance $d_6$ was computed, and $d_6<100\,000$ was satisfied by $105\,853$ cases. At this point the output file was sorted by the value of $d_6$; for example, in the April run there were $2\,337$ cases with $d_6<1\,000$, which appear promising, given the results of the tests of Section 4, and identification check runs were started. Each identification check consisted in an iterative differential correction procedure, attempting to fit the observations of both orbits to a single orbit, starting from the first guess $X_0$ computed with the full linear identification algorithm. During this procedure the automated outlier rejection was turned off to avoid the case--which indeed can occur--that most of the observations from one of the two arcs are rejected; the outliers already removed in the fit of each of the two separate arcs were left out.

The number of cases passing each test in the preceding paragraph are from one particular run performed during the April update, and are given only as an example. In fact we have run the programs numerous times, experimenting with slightly different values of all the controls. The procedure is analogous to the sifting of tons of sand and gravel to find a few gold nuggets. However, the difficulty is not in shoveling tons of gravel: today's computers are so powerful that this amount of data processing (e.g., $\simeq 600\,000\,000$ computations of $d_2$) requires negligible resources (we only have Pentium-based PCs). The main challenge is in achieving full automation of the procedure, and in guaranteeing a very tight quality control.

To stress the importance of high quality work, and before evaluating the practical results, that is the new identifications that we have actually found in this way, we need to point out one main conceptual difference between our search for orbit identifications and the gold mining analogy. Our work is more like the sifting done by todays' tourists, who are allowed to rescan the refuse dumps of the gold rush ghost towns. In fact the data we receive from the MPC have already been scanned for identification by the MPC itself, and to the extent that some information on these data was available before, also by other identification diggers. That we could have found the same identifications found by others has been shown in Section 4, but this is not the point. The big, shiny gold lumps have been found long ago; our methods have to be so much more sophisticated that the identifications which have already escaped all the other methods of detection can be found.

 

	Good	Marginal	Poor	Total
March
Submitted to MPC	104	23	6	133
Published by MPC	104	18	2	124
Credited to us	76	14	1	91
April
Submitted to MPC	14	13	6	33
Published by MPC	14	11	1	26
Credited to us	11	7	1	19

Table 1 contains a summary of the orbit identifications we proposed to the MPC. These are the cases for which we could find a common orbit, to which the observations of both arcs could be fitted with reasonably small (less than $\simeq1.4$ arc-sec) RMS without additional outlier removals. Nevertheless, some of these fits did show systematic errors in the residuals, and were therefore rated either marginal or poor identifications after visual inspection of the residuals with a simple graphics program; some of the marginal and poor cases have not been accepted as identifications by the MPC, but all the cases we rated good have been accepted. Some of the orbit identifications we have proposed have not been published by the MPC under our names, even though they were accepted, because somebody else had proposed them already. Note that this happened in the time span between when the observational data update was made available by the MPC and the date of our submission, that is less than two weeks. This gives an idea of the tight, and indeed stimulating, competition to find asteroid identifications.

The decline in submissions in Table 1 between the March and April updates is due to the fact that the method is new, and there is an initial cleanup with a computational cost that is quadratic in the number of objects tested. We are still working to find optimum filter parameters, so the cleanup continues at a much slower pace; however, at some point the process will switch to a maintenance mode where only objects that have had new observations (or identifications) in the previous month need to be tested. In this mode the computational expense is only linear in the number of objects to be tested.
 

Credited to:	Us	Others
With 1999 designations	17	32
With 1998 designations	51	8
Earlier designations	43	2
Total	110	40

To get a feeling about where the present method is most successful, consider Table 2. Here we distinguish between the 40 identifications which we submitted to the MPC that were credited to others and the 110 identifications that were not found by others. Most of 110 credited discoveries do not include very recent (1999) designations. Conversely, almost all of those which were independently discovered by others are associated with the more recent designations. It is true that the table only reflects those identifications which were obtained from our method, and the 40 that have been discovered by others should not be considered a representative sample of the work done by others in the field. This is especially true in light of the fact that the vast majority of identifications published by the MPC are discovered on the basis of attribution of observations rather than identification of orbits. But, on the other hand, the data from the table indicates that our method is capable of finding some ``difficult'' identifications which have been hiding in the catalogs for a long time.

 

Desig. 1	Desig. 2	$d$	$d_2$	$d_5$	$d_6$	RMS of
						residuals
1997GK16	1989UK7	0.324	0.35	2.27	512.58	0.51
1997CE8	1981PP	0.204	0.07	1800.95	3850.80	0.55
1996YP2	1992RS5	0.194	1.91	95.32	5713.94	0.50
1232T-3	1056T-1	0.159	0.14	161.19	406.52	0.75
1999CT59	1988CY	0.147	1.89	350.39	402.40	0.57
1999CY34	1990SQ7	0.138	6.07	39.87	2005.11	0.77
1999CG86	1993ON8	0.121	4.04	383.90	2004.78	1.07
4868P-L	1997TT11	0.114	0.25	0.74	13848.41	0.28
1998XD29	1997NP	0.111	0.56	6.26	10.73	0.56
1998ST66	1993RG12	0.105	2.90	8.12	8.41	1.18
1997WL37	1993RF4	0.099	17.60	89.70	372.88	1.13
1999FA19	1995DV	0.092	2.89	295.36	305.50	0.64
1131T-2	1998JJ2	0.085	7.39	27.10	7084.67	1.15
1998FS15	1990KF1	0.080	2.32	273.87	278.35	1.41
1998FV87	1978VM9	0.074	0.65	8.30	10.62	1.64
1996VA30	1981UU	0.065	7.61	194.83	891.30	1.27
1998HH52	1983VF7	0.059	1.09	10.92	45771.18	0.81
1998SE7	1994NA3	0.053	0.42	4.64	23.50	0.75
1999CN47	1989GB2	0.047	0.13	13.40	15.65	0.51
1979QZ3	1993QD4	0.042	15.90	1790.95	3172.75	1.25
1999CA73	1993US2	0.040	0.98	34.15	51.42	0.96
1999BP9	1991LN	0.038	0.62	12.07	12.42	0.74
4079T-3	1998VK13	0.034	2.70	4.04	14.64	0.98
1999BG11	1980FC4	0.033	0.99	4.40	4.50	0.59
1998UF40	1991RR26	0.031	0.15	1.90	5.65	0.61
1510T-2	1283T-1	0.029	0.05	7.74	7.87	1.10
1998XW77	1996EP1	0.028	0.05	3.93	4.58	0.70
1999EA5	1997TM26	0.024	1.95	37.09	45.02	1.41
1997TW21	1996HW22	0.023	1.02	83.46	90.35	1.50
9566P-L	1999CN25	0.019	0.25	0.75	40.55	0.57
2234P-L	1998SG8	0.016	0.53	1.01	7.02	0.64
1997MC	1994WP13	0.013	1.11	8.75	10.23	0.92
6705P-L	1998FH6	0.011	0.71	2.15	3.51	0.68
1997WP	1978UE5	0.009	3.48	9.05	9.80	0.77
1999CF66	1996HJ24	0.007	0.77	6.87	6.95	0.61
1993PD7	1970PU	0.005	9.88	14.05	14.46	1.54
2039P-L	1998RZ59	0.002	1.52	3.07	2.10	0.71
4218P-L	1998FF103	0.001	0.16	0.32	0.36	0.44

Table 3 lists a random sampling of the 150 published identifications that were obtained with the present method, though not all of these have been credited to us. A full list of all the orbit identifications that we have proposed can be found online at
http://copernico.dm.unipi.it/identifications/.
One important parameter to evaluate the ``difficulty'' of an identification is the distance of the nominal orbit solutions $X_i=(a_i,h_i,k_i,p_i,q_i,\lambda_i)\, ,\; i=1,2$ being identified. We have sorted Table 3 by a simple distance given by

$$d=\sqrt{\left({\displaystyle a_1-a_2 \over \displaystyle a_1+......\right)^2 +(h_1-h_2)^2+(k_1-k_2)^2+(p_1-p_2)^2 +(q_1-q_2)^2 }$$

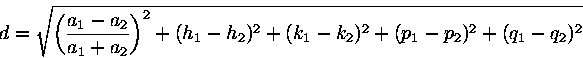
and it is clear that a significant fraction have large $d$ (40 out of 150 accepted identifications have $d>0.1$).

There are some identifications in the Table with high values of $d_6$; the reason for this is that some of the orbit identifications have been proposed because they had low $d_6$, while some had been selected for confirmation by sorting on $d_5$. The value of $d_6$ is most subject to numerical instabilities and to the nonlinearity effects, thus a low $d_5$ couple might be worth checking even if the value of $d_6$ is large.

Many of our proposed identifications involved asteroids recently discovered. This is just the `new lode' effect, that is these orbits had been subjected to a less extensive search for identifications. However, some of these are still quite interesting because of the very long time span between the two observed arcs, for example, we have been credited with discovering three identifications that link asteroids originally discovered during the 1960 Palomar-Leiden survey to objects discovered in 1999. Since many new asteroids are discovered every month, we can expect to continue to find such new cases after each monthly update.

Some of the cases, on the contrary, concerned only orbits of asteroids discovered a long time ago. For example, 1510T-2=1283T-1 and 1232T-3=1056T-1 are identifications of asteroids found in the Trojan surveys T-1 (of 1971), T-2 (of 1973) and T-3 (of 1977): they were not suspected to be the same by the Trojan surveyors, and then they escaped the attention of the MPC and of all the other identification diggers for decades. In 15 of the 150 published identifications both components were discovered before 1995, and all but one of these cases was credited to us. We should not expect to find many more of these `nuggets in the dumps' in the future, unless we further improve our methods, which is, in fact, a work in progress.

6. Conclusions and future THE ASTEROID IDENTIFICATION PROBLEM 4.1 Test on 100