Definición 2.1
Una relación
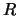
entre los conjuntos
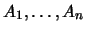
es cualquier subconjunto
Los conjuntos
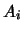
son los dominios de la relación,
el número de elementos de
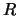
se llama cardinalidad,
y el número
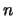
se denomina grado de
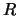
.
Para indicar explícitamente la relación es de grado
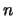
,
se dice también que
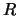
es una relación
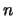
-aria.
Nota 2.2 (Lógica y relaciones)
Existe un tipo de lógica llamada `` Lógica Relacional'',
basada en relaciones de grado
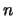
. Esta Lógica tiene interés
en la construcción de `` Bases de Datos Deductivas'',
que se emplean en el diseño de `` Sistemas Expertos''
(Inteligencia Artificial).