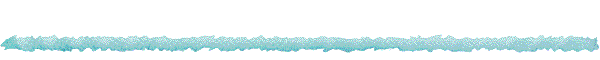
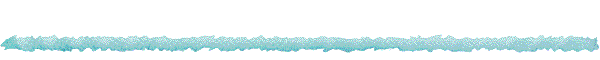
Índice

(Este mismo índice aparece en el marco de la izquierda para facilitar consultas sucesivas)

		Los números naturales  El principio de inducción matemática División exacta y división entera Descomposición en factores primos  Máximo común divisor y mínimo común múltiplo. Algoritmo de Euclides Representación de un número natural en una base cualquiera
		Los números enteros
		Los números racionales Relación de orden en el conjunto de los racionales Densidad del conjunto de los racionales.  Propiedad arquimediana Cardinal de los racionales Representación decimal de los números racionales
		Los números irracionales
		Los números reales

Volver a página principal

Los números naturales

Los números naturales surgen de la necesidad de contar, de enumerar: ={1,2,3,4...}

• Con los números naturales  se puede sumar. De hecho, con la operación suma, los naturales forman un semigrupo conmutativo.
• Con la operación producto los naturales también tienen estructura de semigrupo conmutativo.
• El infinito de los números naturales se denomina infinito numerable. Cualquier conjunto que pueda ponerse en correspondencia biyectiva con el conjunto de los números naturales se dice que es infinito numerable. Por ejemplo, el conjunto de las potencias sucesivas de un número  , es decir, el conjunto   cuando  es distinto de 0, 1 y -1, es un conjunto infinito numerable. El conjunto de los números enteros y el de los racionales también son infinitos numerables como se verá más adelante.
• El conjunto de los naturales es un conjunto totalmente ordenado, es decir, existe una relación de orden total, lo que significa que existe una relación de orden y que dos elementos cualesquiera pueden ser siempre comparados entre sí usando dicha relación. Dicho de otra forma, dados dos naturales, e , o bien , o bien.
• Todo subconjunto no vacío del conjunto de los naturales tiene un elemento mínimo, esto es, existe un elemento tal que para todo de se tiene .
  Por ejemplo, el subconjunto formado por los números pares tiene como elemento mínimo a 2.
• Principio de inducción matemática: si un subconjunto de verifica que y, si , resulta que , entonces .
  
  • Esto nos permite realizar razonamientos por inducción cuando queremos probar que una determinada propiedad se cumple para todo natural. Por ejemplo, si queremos probar que la suma de los primeros números naturales es podemos hacerlo por inducción en la forma siguiente:
    

    Para es claro que la suma de los 1 primeros números naturales es .
    Suponiendo cierta la fórmula para , es decir, , veamos que también es cierta para ,

    

    Luego la fórmula es válida para todo n natural.

  • Ejercicio: Demostrar, razonando por inducción, las siguientes fórmulas:
    
    • 
    • 
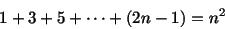
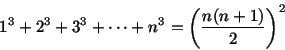
• Dados dos números naturales , no es cierto en general que exista un natural tal que . Si tal existe se denomina cociente exacto de por , y la división se denomina exacta. En este caso se dice que es divisible por , o que es un divisor de , o que es un múltiplo de .
  Cuando no es así, siempre es posible encontrar y que verifiquen con Los números , , y se denominan dividendo, divisor, cociente y resto respectivamente y el procedimiento para determinar y a partir de y se denomina división entera.
   
• Descomposición en factores primos:
   
  Un número primo es aquél número natural que sólo es divisible por sí mismo y por la unidad, por ejemplo 2, 3, 5, 7, 11, 13, 17, 19, 23, ..., son números primos.

  Hay infinitos números primos. Un famoso procedimiento para encontrar números primos es la denominada criba de Eratóstenes, que consiste en tomar una lista de los números naturales e ir tachando sucesivamente los múltiplos de cada natural que aún no hubiera sido tachado previamente.
   
  

  

  
  
  
  
  El uso de números primos grandes tiene aplicaciones en criptografía (ocultación de secretos).

  Todo número natural admite una descomposición en producto de números primos. Esta descomposición es única salvo el orden de los primos considerados. En el siguiente recuadro tienes algunos ejemplos.

  

  Encontrar la factorización de números grandes es un problema con elevada complejidad computacional, de hecho no hay ningún algoritmo eficiente para ello. Por eso varios sistemas criptográficos se basan en este problema.
   
   

• Máximo común divisor y mínimo común múltiplo. Algoritmo de Euclides.
  
  El máximo común divisor de dos números se define, como su propio nombre indica, como el divisor más grande que ambos números tienen en común. Si disponemos de la factorización de ambos números, entonces el máximo común divisor se obtiene quedándose solamente con aquellos factores comunes a ambas descomposiciones y elevados al menor de los exponentes con los que aparezcan.

  El mínimo común múltiplo, nuevamente como indica su nombre, es el múltiplo más pequeño que ambos números tienen en común. Atendiendo a las descomposiciones de ambos números, el mínimo común múltiplo se obtiene considerando todos los factores distintos que aparecen (comunes y no comunes), cada uno de ellos elevado al mayor exponente con el que aparezca.

  
  
  

  Según se dijo antes, calcular la factprización deoun número es un proceso muy costoso. Sin embargo, puede calcularse el máximo común divisor de dos números de una manera eficiente, sin necesidad de factorizar previamente ambos números. Es lo que se conoce como algoritmo de Euclides y consiste en lo siguiente:
   

  • Dados dos números , comenzamos relizando la división entera de entre .
  • Cada paso consiste en una nueva división, en la que el dividendo es el número que actuó de divisor en la división anterior y el divisor es el número que se obtuvo como resto en la división anterior.
  • Cuando en una división se obtiene resto nulo, el máximo comun divisor de los números de los que partimos será el número que ha actuado como divisor en esa última división efectuada y que resultó ser una división exacta.
    
    

  
  

  
  
  Una vez obtenido el máximo común divisor de esta manera, ¿se te ocurre cómo obtener el mínimo común múltiplo sin necesidad de factorizar los números?
   
   
• Representación de un número natural en una base cualquiera:
  
  El método de divisiones enteras sucesivas permite escribir cualquier número natural en forma única en una base cualquiera p, en la forma siguiente:
  
  
  en base p, donde .

  Para lograr dicha expresión basta con realizar sucesivas divisiones enteras de n por p y tomar los restos, es decir,

  

  hasta que en la r-ésima divisón, se tenga . Se toma , y hemos terminado.
   

  • Nótese que nuestra actual notación posicional para los números naturales se corresponde con la representación de los números naturales en base decimal (p=10). Se denomina notación posicional porque el valor de una cifra depende de la posicón que ésta tenga en el número: un 5 en el lugar de las unidades vale 5, mientras que en el lugar de las centenas vale 500.
  • La notación binaria, tan común en el mundo de la informática es el resultado de tomar p=2 y representar los números naturales en dicha base.
  • ¿Conoces otras representaciones en bases distintas? Hexadecimal, sexagesimal...

Los números enteros

Cuando se necesita además restar surgen los números enteros ={ ... -3, -2, -1, 0, 1, 2, 3, ...}

• Los enteros se obtienen a partir de los naturales añadiendo los opuestos para la operación suma.
• Si a y b denotan números naturales, la suma de dos números enteros a+(-b), se define como:
  
  
  el entero positivo a-b, si a > b,
  0, si a=b
  el entero negativo -(b-a) si a < b
  
  La suma de dos enteros negativos se define como (-a)+(-b)=-(a+b)
  
  De hecho, los enteros, con la operación suma tienen estructura de grupo conmutativo.
  
• Si además de la suma, consideramos la operación de multiplicación definida como
  
  • (-a)(-b)=ab
  • (-a)b=a(-b)=-(ab),
  
  el conjunto de los enteros, con ambas operaciones tiene estructura de anillo conmutativo y con unidad.
• Por cierto, ¿qué hay más?, ¿números enteros o números naturales?. Nótese que se puede establecer una correspondencia biyectiva entre ambos conjuntos, , por ejemplo como ésta:
  
  
  si n es un entero positivo
  
  
  Por tanto, el conjunto de los enteros es también infinito numerable. También es un conjunto totalmente ordenado, cuando se considera la relación de orden definida en la forma obvia y que extiende la relación de orden que se tiene en . También es cierto que en los enteros todo subconjunto acotado inferiormente tiene elemento mínimo, y recíprocamente, todo subconjunto acotado superiormente tiene elemento máximo.

Los números racionales

Si se necesita además dividir, surgen los números racionales (o fraccionarios, o quebrados), ={... 1/2,  5/3,  8/10,  238476/98745, ...... }

• Los racionales se obtienen a partir de los enteros añadiendo los inversos para la multiplicación.
  • La suma de dos racionales a/b y c/d se define como a/b+c/d=(ad+cb)/bd.
  • El producto de dos racionales a/b y c/d se define como ac/bd.
  • Dos números racionales a/b y c/d son iguales si y sólo si ad=bc.
    
       (En todo lo anterior, a, b, c y d denotan números enteros)
    
  • Un número racional se dice que está expresado mediante una fracción irreducible si el numerador y el denominador no tienen factores comunes.
  De este modo, el conjunto de los racionales, con las operaciones de suma y producto tiene estructura de cuerpo conmutativo.
• En se pueden resolver todas las ecuaciones lineales, es decir, aquéllas de la forma ax+b=0, con a y b racionales.
• En se puede definir un orden total compatible con las operaciones suma y producto definidas anteriormente y que extienda el orden existente en y en . Para ello basta con definirlo como sigue:
  
  
  Dados dos números racionales a/b y c/d, donde b y c son enteros positivos (esto siempre puede conseguirse, por ejemplo, si b es negativo basta con multiplicar a y b por -1 para obtener un número racional igual que el dado pero con denominador positivo), se dice que si y sólo si respecto del orden existente en el conjunto de los enteros.
  
  Por tanto con dicho orden es un conjunto totalmente ordenado.

 
• Densidad del orden:
  Dados dos números racionales distintos, , siempre existe otro número racional tal que .
  
  Para ello, si    , con  b y d positivos, basta con tomar 
  
  Ejercicio: probar que efectivamente  (por ejemplo, entre  3/5 y 2/3 se encuentra 5/8)
  
  Ahora bien, reiterando el proceso de intoducir un racional entre cada dos racionales distintos es claro que entre dos racionales distintos existen infinitos racionales distintos,
   
  Por ejemplo, ahora entre 3/5 y 5/8 se encuentra 8/13, entre 3/5 y 8/13 se encuentra 11/18, etc., tenemos asi 3/5 < ...... < 11/18 < 8/13 < 5/8 < 2/3.
  
  por eso se dice que el conjunto de los racionales es un conjunto denso. No tiene sentido hablar del racional siguiente o anterior a uno dado. Esto es algo que no ocurría ni en el conjunto de los naturales ni en el de los enteros.
   
• Propiedad arquimediana (o de Arquímedes):
  Dados dos números racionales y , siempre existe un n natural tal que .   Esto quiere decir que por pequeño que sea , si consideramos la sucesión de racionales , llegará un momento en que sobrepasasaremos a , por muy grande que este sea.
  
  Por ejemplo:

  

  Esta es una propiedad que también poseían los números naturales y los enteros.
   
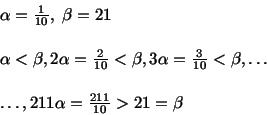
• El cardinal de los racionales:
  ¿Cuántos números racionales hay? ¿Qué hay más, naturales o racionales?
  
  Puede parecer que la respuesta sería, obviamente hay más racionales, puesto que los naturales son también números racionales, y además hay otros racionales, como 1/2 por ejemplo, que no son naturales, por lo que podemos concluir que el cardinal de los racionales es que el de los naturales.

  Pero podemos también probar que hay más naturales que racionales. Una forma de hacerlo sería seguir el siguiente razonamiento gráfico. Coloquemos los enteros en un eje horizontal, y también en un eje vertical. Cada punto (a,b) del retículo que se forma representará al racional a/b. Comenzamos ahora a trazar un camino en espiral, partiendo del origen que recorra uno a uno todos los puntos del retículo como se ve en la siguiente gráfica:
   
   

  

  
  Es claro que podemos poner en correspondencia biyectiva los puntos del retículo con los naturales sin más que irlos numerando a medida que la linea espiral pasa por cada uno de ellos. Ahora bien, no todos los puntos del retículo se corresponden con números racionales, ya que los de la forma (n,0) no se corresponden con ningún racional, y además muchos puntos del retículo representan al mismo número racional, por ejemplo (1,2) y (2,4) representan al mismo número racional, ya que 1/2=2/4. De aquí se concluye que podemos dar una correspondencia sobreyectiva de  en , y por tanto que el cardinal de  es  que el cardinal de .

  Combinando ambos resultados podemos concluir que el cardinal de  es igual que el de , es decir, que  es un conjunto infinito numerable.

  Ejercicio: encontrar un correspondencia biyectiva entre  y .



• Representación decimal de números racionales:
  
  Todo número racional admite una representación decimal, que es la que se obtiene al dividir el numerador entre el denominador, por ejemplo 1/2 tiene como expresión decimal 0.5 ,     3405/25=136.2  y 1/3= 0.33333.......

  Esto puede dar lugar a dos tipos de expresiones decimales, las exactas y las periódicas. Éstas últimas pueden a su vez dividirse en periódicas puras o periódicas mixtas.

  
  
  • Expresión decimal exacta, es aquélla que tiene un número finito de términos. Por ejemplo: 0.5,    1.348  ó    367.2982345
    Esta expresiones surgen de números racionales cuyo denominador (en la expresión irreducible) sólo contiene los factores 2 y 5. Por ejemplo 1349/1000, 40/25, ...
  • Expresión decimal periódica es aquélla que tinene un número infinito de cifra decimales, pero de modo que un grupo finito de ellas se repite infinitamente, de forma periódica, por ejemplo 0.333333.....,    125.67777777.......  ó    3.2567256725672567......
    Surgen de fracciones cuyo denominador contiene factores distintos de 2 y 5, por ejemplo, 1/3=0.33333.....
    La parte que no se repite se denomina anteperíodo y la que se repite, período.
    • Periódica pura es aquélla que no tiene anteperíodo.
    • Periódica mixta es aquélla que sí tiene anteperíodo.
    Podría considerarse que las expresionas decimales exactas son periódicas mixtas pero con período 0.

    
    
    

    Recíprocamente, dada una expresión decimal exacta o periódica, puede encontrarse una expresión racional para la misma siguiendo la siguiente norma:

    
     
    • Si la expresión es exacta se coloca como numerador el número entero que resulta de suprimir el punto decimal y como denominador la unidad seguida de tantos ceros como cifras se encontraran a la derecha del punto decimal en la expresión decimal original.
    • Si la expresión es periódica, se coloca como numerador el resultado de restar al número entero formado por el anteperíodo seguido de la primera repetición del período, el entero formado por el anteperíodo, todo ello multiplicado por la unidad seguida de tantos ceros como cifras significativas se encuentren a la izquierda del punto decimal. Como denominador tantos nueves como cifras tenga el período seguidos de tantos ceros como cifras tenga el anteperíodo.
      
      

    
    Ejemplos:
    
    

    

    
    Posteriormente se pueden simplificar las fracciones obtenidas para conseguir la expresión irreducible.

  

  
  

Los números irracionales

Hay números que no son racionales, es decir que no pueden ser expresados como cociente de dos números enteros. Por ejemplo, piensa en el número cuya representación decimal es

0.1234567891011121314151617181920........

claramente, esta representación decimal no es exacta ni periódica, por tanto no puede corresponderse con ningún número racional.

Veamos otros ejemplos.

Se trata de un ejemplo típico de número no racional con una demostración muy sencilla de que, en efecto, no puede ser racional

En el siguiente recuadro puedes ver las primeras 100 cifras decimales de . Además se muestra una manera de construir el número  sobre la recta real con regla y compás y finalmente se da una serie de números racionales que converge hacia .
 
 

Para construir la serie que converge hacia  hemos usado obviamente la sucesión de cifras decimales indicada más arriba. También podíamos haber definido una sucesión de números racionales que converge hacia de la forma siguiente

donde  es el mayor número entero que verifica .

p
Otro de los ejemplos cásicos de números irracionales que estamos acostumbrados a manejar es el conocido por la letra griega Pi que representa la relación entre el perímetro y el diámetro de una circunferencia.

A diferencia de lo que ocurre con , no es posible dibujar con regla y compás el número  sobre la recta real. El problema es conocido como la rectificación de la circunferencia y hay métodos algebraicos para demostrar que no tiene solución, a pesar de que mucha gente la buscó durante siglos (y algunos siguen buscándola hoy en día). Otros problemas de parecida índole son los famosos de la cuadratura del círculo, que consiste en construir con regla y compás un cuadrado que tenga el mismo área que un círculo dado, y la trisección del ángulo, que consiste en dividir un ángulo dado en tres partes iguales. Todos ellos son imposibles con regla y compás y puede demostrarse algebraicamente su imposibilidad.

En el siguiente recuadro tienes las primeras cien cifras decimales de y además una serie de números racionales que converge hacia .

La serie indicada es conocida como serie de Leibniz y hemos de advertir que su convergencia es bastante lenta. ¿Cuántos términos te hace falta sumar para obtener 10 cifras decimales correctas?

También el número , base de los llamados logaritmos naturales o neperianos es un número irracional. Este número surge de forma natural al considerar el interés compuesto.

Supongamos que tenemos un capital unidad a un interés anual  (en tanto por uno). Al cabo del año nuestro capital será .

Sin embargo, si dividimos el año en dos semestres e incorporamos el interés al finalizar cada uno dos semestres, al final del primer período tendremos  y al finalizar el año 

Si dividimos el año en tres cuatrimestres, incorporando los intereses al capital al final del cada período, tendremos  respectivamente al final de cada cuatrimestre.

...

Si dividimos el año en n períodos tendremos al final del año .

Se define  como el límite del resultado anterior cuando n se hace infinitamente grande (infinitos períodos infinitamente pequeños), siendo , es decir

En el recuadro siguiente vemos las 100 primeras cifras decimales de , así como dos formas de ver  como límite de sucesiones de números racionales (en el segundo caso se trata de una serie).

Igual que pasaba con , no es posible dibujar con regla y compás un punto en la recta real a distancia del origen.

Si consideramos el conjunto de todas las expresiones decimales, solamente aquéllas finitas o periódicas se corresponderán, como ya se vio, con números racionales; el resto forman el conjunto de los números irracionales.
El conjunto de los irracionales, denotado por  tiene, como , la propiedades de orden total, densidad y propiedad arquimediana. En cambio  no es un conjunto numerable. ¿Se te ocurre alguna forma de probar que  no es numerable?

(pincha aquí para ver una forma de demostrarlo)

Ya se ha visto para los ejemplos mostrados, pero se puede afirmar en general que todos los números irracionales pueden verse como límites de sucesiones de números racionales. Para ello basta con considerar la expresión decimal del número en cuestión y construir la sucesión obvia que consiste en considerar cada vez un cifra decimal más, de modo que el término  es la fracción que da lugar a la expresión decimalm exacta formada por las n primeras cifras del número dado.

Los números reales

La unión de los racionales y los irracionales forma el conjunto de los números reales. .

El conjunto de los reales, con el orden inducido por el orden ya visto en ,   y   es un conjunto totalmente ordenado.

Teniendo eso en cuenta, se puede representar gráficamente el conjunto de los reales con una recta, en la que cada punto representa un número.

Muchas de las propiedades que hemos visto para los conjuntos  e  son heredadas por .

Como ya se ha visto,  es denso en  . También  es denso en .

Podemos considerar  como el conjunto de todos los límites de sucesiones cuyos términos son números racionales.

A diferencia de lo visto para ,  y , el conjunto de los reales no es numerable. (una demostración).

Veamos por último un cuadro resumen de las propiedades que hemos analizado en los distintos conjuntos de números.
   

	Ordenado	Denso	Numerable	Estructura algebraica
				+   Semigrupo *   Semigrupo
				+      Grupo *      Semigrupo +,*   Anillo conmut. con1
				+      Grupo *      Grupo +,*   Cuerpo conmut.
				No tiene estructura algebraica al no ser cerrado para + y *
				+      Grupo *      Grupo +,*   Cuerpo conmut.

Página creada por Angela Barbero Díez