Vamos a demostrar que  no es numerable, y para ello vamos a considerar únicamente los números reales entre 0 y 1 y vamos a ver que ellos ya forman un conjunto no numerable, por lo que el conjunto total de los reales será ciertamente no numerable ya que contiene un subconjunto no numerable.

El conjunto de todos los números reales entre 0 y 1 está formado por todas las expresiones decimales que tienen 0 como parte entera (es decir, la parte a la izquierda de la coma decimal).

Razonemos por reducción al absurdo y supongamos que sí pueden numerarse dichas expresiones decimales.

Denominemos  a la primera de ellas,   a la segunda, etc, de modo que la corrrespondencia    es biyectiva.

.

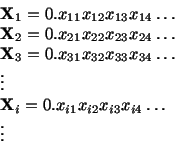
Definimos ahora para cada n 

Consideremos la expesión decimal .............

Obviamente  está entre 0 y 1, luego debe existir algún  tal que , pero vemos que esto no es posible ya que la -ésima cifra decimal de  es , que es obviamente distinta de la -ésima cifra decimal de , que es 

Nótese que, teniendo en cuenta que , el hecho de haber probado que el conjunto de los rales es no numerable y el de los racionales numerable, automáticamente implica que el conjunto de los irracionales ha de ser no numerable.