Enunciado del Problema

Las regiones y del plano XY están conectadas por medio de un puente que se ha construido trasladando la curva de ecuación z=cos(x)+1 contenida en el plano y=-1 paralelamente al eje Y (desde y=-1 hasta y=1). Se pide:

  1. Realícese un dibujo que represente el puente anteriormente descrito.
  2. Constrúyase una parametrización regular de la superficie del puente.
  3. Calcúlese la primera forma fundamental en la parametrización dada en el apartado 2.
  4. Plantéese una integral para calcular el área de la superficie del puente y aproxímese su valor empleando la regla de Simpson.
  5. Un vehículo cruza el puente de tal forma que la proyección de su recorrido sobre el plano XY viene dada por la curva de ecuación y=sen(x). Calcúlese la longitud de la trayectoria descrita por el vehículo.
  6. Calcúlese el ángulo formado por la trayectoria del vehículo anterior en el punto de abscisa x=0 con la correspondiente x-curva.
  7. Para el campo
                                   
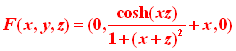
    calcúlese el flujo del rotacional de F a través de la superficie del puente orientada de forma que la tercera componente del vector normal sea negativa.
     

  8.  
    		9.

  9.  
    		10.

  10.  
    		11.

  11.  
    		12.

  12.  
    		13.

Regreso a la página de instrucciones