Cálculos correspondientes al apartado 3)
En este apartado se vuelve a pedir calcular el trabajo realizado
por un campo de fuerza sobre una partícula que se desplaza a lo largo de una curva,
se trata por tanto de una integral de línea de un campo vectorial.
Pero ahora ya sabemos por el apartado anterior que se trata de un campo conservativo.
Consideraciones sobre la trayectoria de la partícula
Nuevamente en el enunciado se observa que no se determina ninguna trayectoria particular para el copo de nieve, lo que se da son los puntos inicial y final de dicha trayectoria, que sabemos que son suficiente para determinar el valor del trabajo por ser el campo conservativo. Un dibujo aproximado de la situación descrita podría ser el siguiente:
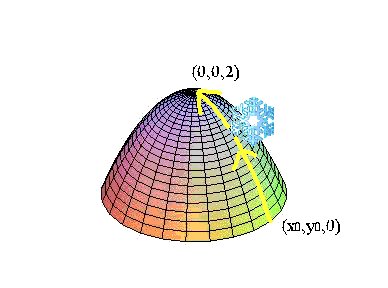
Posibles formas de resolver el problema
Una opción sería tomar cualquier trayectoria que uniera esos dos puntos,
por ejemplo una línea recta, parametrizarla y calcular la integral
de línea correspondiente (prueba a resolverlo de esta forma y compara
tu resultado con el obtenido aquí).
Nosotros vamos a tomar otra opción. El hecho de que el campo sea conservativo
es equivalente a que sea un campo gradiente, es decir, gradiente de una función de potencial.
Si conocemos dicha función de potencial bastará con evaluarla en los extremos
de la curva para tener el valor de la integral de línea pedida.
Cálculo de la función de potencial del campo
Si 
es
la función de potencial del campo F,
entonces se tiene la siguiente relación:
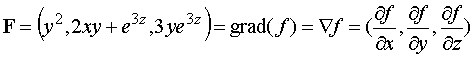
Por tanto, igualando componente a componente, tenemos
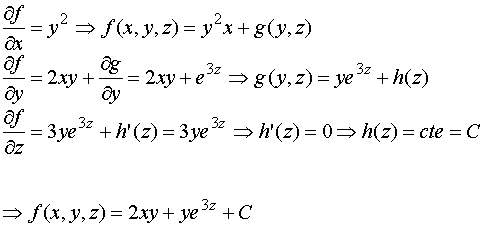
Cálculo del trabajo
Finalmente, el trabajo realizado por el campo de fuerza para desplazar
el copo desde el punto
hasta el punto
viene dado por:
Otras consideraciones
Observamos que el signo que tome el valor del trabajo será positivo o negativo dependiendo del punto base del que se parta, por lo que se deduce que el campo ayudará o impedirá el que el copo suba desde la base hasta la cima del iglú dependiendo del punto de partida que se elija.