Cálculos correspondientes al apartado 1)
En este apartado se pide calcular el flujo de calor a través de la superficie y el suelo del iglú. Se trata, pues de una integral de superficie de un campo vectorial. podemos distinguir varios pasos en el proceso:
Determinación del campo que se ha de integrar
Primero tenemos que determinar el campo cuyo flujo se quiere calcular. El dato proporcionado es la función de distribución de temperatura
Por Física sabemos que, dada una distribución de temperatura, el flujo de calor viene dado por la ecuación
En nuestro caso tenemos
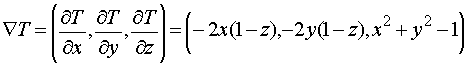
Tomando 
como se indica en el enunciado, tendremos
Consideraciones sobre cálculo vectorial
Nuestra superficie es la unión de dos trozos bien diferenciados:
la superficie del iglú, que se trata del paraboloide elíptico dado por la ecuación del enunciado
el suelo, que se trata de la porción correspondiente del plano 
La integral total será la suma de las integrales a través de las dos superficies indicadas.
Ahora bien, la unión de ambas superficies forma una superficie cerrada que encierra una porción
del espacio. Y por ser el campo de clase 
(todas sus componentes son funciones derivables con respecto a todas las variables) podemos hacer uso del teorema de la divergencia
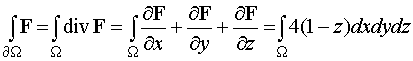
Cálculo de la integral
En principio basta con estimar los límites de integración en cada variable y realizar la integral triple que resulta. Sin embargo, por la geometría del cuerpo observamos que será más fácil describirlo en coordenadas cilíndricas que en cartesianas, por lo que usaremos el teorema de cambio de variables para integrales triples. Las ecuaciones del cambio de cartesianas a cilíndricas son las siguientes:
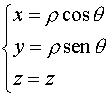
siendo el determinante Jacobiano de la matriz de cambio de coordenadas
r .
Teniendo en cuenta que la ecuación de la superficie del iglú es 
tendremos que la nueva integral, con los límites de integración en cada variable correctamente determinados es la siguiente
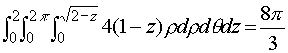
este último valor es el resultado pedido en el apartado 1 del problema que queda así completado
Otras consideraciones
Teniendo en cuenta que en el teorema de la divergencia se considera que la superficie que delimita el cuerpo está orientada con la normal exterior, el hecho de que el resultado de la integral calculada sea positivo indica que el calor fluye en la dirección de la normal, es decir desde dentro del iglú hacia fuera del mismo. Lo que no sabemos es qué parte fluye a través de las paredes y qué parte a través del suelo. Si se quisiera conocer esto tendríamos que parametrizar una de las dos superficies (por ejemplo el suelo, por ser más sencilla) y realizar la integral de flujo sobre la superficie correspondiente. Hay que tener siempre exquisito cuidado con la orientación que induce la parametrización elegida, puesto que la integral de flujo es una integral orientada.