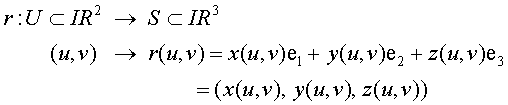
Teoría local de superficies

Representación paramétrica

Definición Se denomina representación (bi)paramétrica regular de clase C^m (m ≥1) de una superficie S en el espacio IR³ a toda aplicación suprayectiva

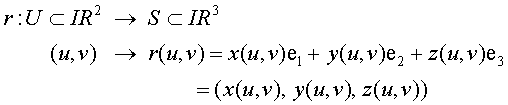
tal que r Є C^m(U)  y  r_u(u,v) Λ r_v(u,v) ≠ 0 para todo (u,v) Є U.

Si se toma en U el conjunto definido por v=v₀ (un trozo de recta paralela a uno de los ejes en  IR²) su imagen sobre S será la curva r=r(u,v₀), parametrizada por u, que se denomina u-curva v=v₀ . Análogamente, la imagen de u=u₀ será la curva r=r(u₀,v), parametrizada por v, que se denomina v-curva u=u₀ .

Definición Las u-curvas y v-curvas se denominan curvas paramétricas o curvas coordenadas de la superficie. Por cada punto de la superficie pasa una u-curva y una v-curva.

Definición Para un punto P=r(u,v) de la superficie,  (u,v) reciben el nombre de coordenadas curvilíneas de P.

Si se tiene una parametrización regular r de una superficie S los vectores r_u(u,v)  y r_v(u,v) son linealmente independientes y en cada punto generan un plano que se conoce como plano tangente a la superficie. En este caso se tiene definido el vector normal al plano.

Definición El vector unitario

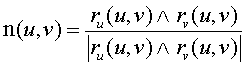
  es normal al plano tangente en el punto r(u,v) y se conoce como vector normal a la superficie en dicho punto.

Cambios admisibles de parámetro

Definición Una transformación f 

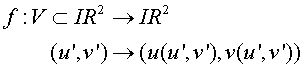
es un cambio admisible de parámetros de clase C^m (m ≥1) si

1.- f es de clase C^m en V y f(V)=U,

2.-   

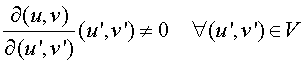
La relación entre los vectores normales asociados a dos parametrizaciones regulares r y r' que se relacionan mediante un cambio admisible de parámetros viene dada por

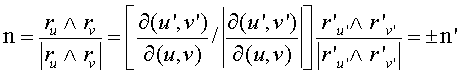
lo que indica que la dirección del vector normal es invariante aunque el sentido puede cambiar dependiendo del signo del jacobiano de la transformación f.

Carta local y atlas sobre una superficie

A veces no es posible dar una parametrización regular para toda la superficie. En tal caso cabe la posibilidad de conjugar distintas parametrizaciones regulares para representar la superficie, cada una de las cuales cubrirá una parte de la misma. Esta idea se formaliza mediante el concepto de carta local y atlas.

Definición Se llama carta local de clase C^m (m ≥1) en S a toda aplicación r: U ―>S con U abierto tal que

1.- r Є C^m(U) ,

2.- r_u Λ r_v ≠ 0 en U,

3.- r es inyectiva y bicontinua (ella y su inversa son continuas) en U.

De este modo una carta local es una representación paramétrica regular inyectiva y bicontinua de una parte de S.

Cuando se tenga una colección de cartas locales de clase C^m que cubren toda la superficie, de forma que si la intersección de dos cartas es no vacía las parametrizaciones de ambas cartas se relacionan mediante un cambio admisible de parámetros, entonces diremos que se tiene un atlas A sobre la superficie. El par (S,A) se denomina superficie simple.

Superficie orientable y superficie orientada

Definición Una superficie se dice que es orientable si el sentido del vector normal se conserva.

Cuando la superficie está definida mediante un atlas, si la superficie es orientable el cambio de carta no debe suponer un cambio en el sentido del vector normal.

La banda de Moebius es un ejemplo de superficie no orientable.

Definición Una superficie orientable está orientada cuando se ha fijado un sentido para el vector normal.

Primera forma fundamental

Dada una carta local r de clase C^m de una superficie S, el plano tangente en un punto r(u,v) está generado por los vectores r_u(u,v)  y r_v(u,v)   y cualquier vector tangente en ese punto se podrá expresar como combinación lineal de los anteriores.

Así, si se tiene una curva sobre la superficie l(t)=r(u(t),v(t)) su vector tangente l'(t) será r_uu'(t) + r_vv'(t), que se puede escribir independientemente del parámetro t como r_udu + r_vdv.

Como todos los vectores del plano tangente en un punto se pueden ver como tangentes a alguna curva contenida en la superficie, se podrán escribir como dr= r_udu + r_vdv.

Definamos los primeros coeficientes fundamentales como

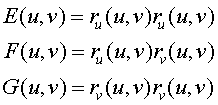
Utilizando los coeficientes anteriores tenemos

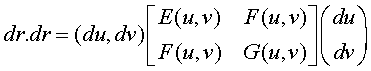
donde dr=r_udu + r_vdv.

Definición Se denomina primera forma fundamental de la superficie a

Propiedades de la primera forma fundamental

1.- I es invariante por cambios admisibles de parámetros, es decir, es independiente de la parametrización.

2.- I define una forma cuadrática definida positiva en el espacio tangente en cada punto.

3.- I permite calcular longitudes, ángulos y áreas sobre la superficie.

Cálculo de longitudes

Dada una curva regular sobre la superficie r(u(t),v(t)), la longitud del arco de curva de t₀ a t₁ viene dada por

Cálculo de ángulos

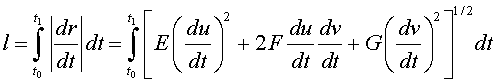
Dados dos vectores dr y dr^* del espacio tangente a la superficie en un punto, el ángulo que forman viene dado por

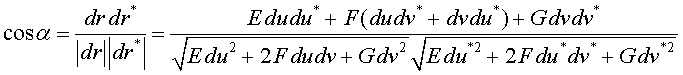
En particular, el ángulo β que forman en un punto las curvas paramétricas (vectores tangentes (0,dv) y (du^*,0)) será

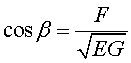
de forma que las curvas coordenadas son ortogonales si F=0.

Cálculo de áreas

El área del trozo de superficie que es imagen del conjunto U, es decir, el área de r(U) viene dado por

Segunda forma fundamental

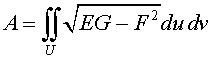
Dada una carta local  r=r(u,v) de una superficie de clase C^m (m ≥2), se define la segunda forma fundamental asociada como

donde e, f y g se conocen como segundos coeficientes fundamentales y  vienen dados por

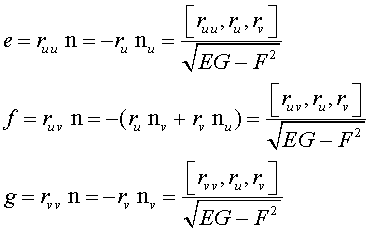
 Propiedades de la segunda forma fundamental

1.- II es invariante frente a cambios admisibles de parámetro que conservan la orientación.

2.- II permite definir el paraboloide osculador de la superficie en cada punto y, atendiendo a su naturaleza, clasificar los puntos de la superficie.

Tenemos los siguientes casos:

Caso elíptico:  eg-f² > 0,  el paraboloide osculador es un paraboloide elíptico.

Caso hiperbólico: eg-f² < 0,  el paraboloide osculador es un paraboloide hiperbólico.

Caso parabólico:  eg-f² = 0 con e²+f²+g² ≠ 0,  el paraboloide osculador es un cilindro parabólico.

Caso planario:  e = f = g = 0  no hay paraboloide osculador