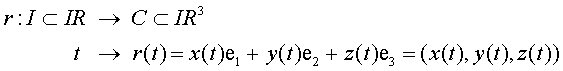
Teoría local de curvas
Definición Se denomina representación paramétrica de una curva C en el espacio IR3 a la aplicación
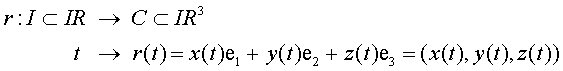
Definición Se denomina representación paramétrica regular de clase Cm (m ≥1) de una curva C a toda aplicación suprayectiva
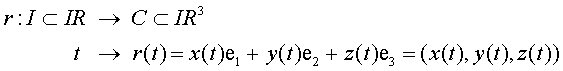
tal que r Є Cm(I) y r'(t) ≠ 0 para todo t Є I
Nota
![]()
La condición r'(t) ≠ 0 equivale geométricamente al hecho de que exista la recta tangente a la curva en el punto r(t0) que vendrá definida como
![]()
Cambio admisible de parámetro. Curva regular y curva regular orientada.
Definición Se dice que un cambio de parámetro
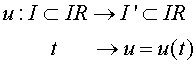
es admisible de clase Cm (m ≥1) si
1.- u es de clase Cm en I
2.-
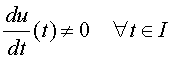
Como consecuencia de la definición se tiene que la aplicación u es inyectiva en J=u(I) y su inversa u-1 también es un cambio admisible de parámetro en J.
Definición Dos representaciones paramétricas regulares de clase Cm de una curva, r(t) y r(u), se dice que son equivalentes si se relacionan mediante un cambio admisible de parámetro de clase Cm u=u(t) tal que u(I)=J y r(u(t))=r(t) con t Є I.
De esta forma se tiene una relación de equivalencia sobre el conjunto de las representaciones paramétricas regulares de clase Cm , lo que permite definir el concepto de curva regular como una clase de equivalencia de las representaciones paramétricas regulares.
Una parametrización de una curva C define sobre ella un sentido (de recorrido). Dos representaciones paramétricas de una misma curva relacionadas mediante el cambio admisible de parámetro u(t) definen el mismo sentido sobre la curva si
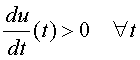
Se dice entonces que el cambio de parámetro preserva la orientación. En caso contrario diremos que cambia la orientación.
De esta manera podemos definir una nueva relación de equivalencia sobre las representaciones paramétricas regulares: dos parametrizaciones son equivalentes si están relacionadas mediante un cambio de parámetro que conserva la orientación. Una curva regular orientada será una clase de equivalencia determinada por la relación anterior. De esta forma:
Definición Se llama curva regular orientada a una curva regular para la que se ha elegido un sentido especifico.
Parametrización natural. Parámetro longitud de arco.
Definición Dada una representación paramétrica regular r de una curva C se define su longitud l entre los puntos de la curva r(t0) y r(t1) como
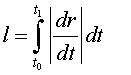
La longitud no depende de la parametrización.
Definición Dada una parametrización regular r(t) de una curva regular en un intervalo I, y t0 Є I, sea
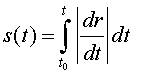
s=s(t) se denomina parámetro longitud de arco a lo largo de r y mide la longitud del arco de la curva, con signo, comprendido entre los puntos r(t0) y r(t1).
Definición Una parametrización r(s) de una curva regular se dice que es natural si verifica
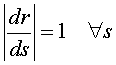
La parametrización mediante la longitud de arco es una parametrización natural.
Teorema Si r=r(s) con s Є I es una parametrización natural de una curva C, entonces
1.- |s1- s2| es la longutud del arco de C comprendido entre r(s1) y r(s2).
2.- Si r=r(s) con s Є J ese otra representación natural de C, entonces s=±s+constante.
3.- Si r=r(s) con s Є I tiene la
misma orientación que r=r(s)
s Є
J entonces
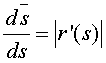
En caso contrario
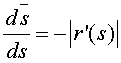
Sea r=r(s) con s Є I una parametrización natural de una curva C de clase C3. Como s es un parámetro longitud de arco se tiene
![]()
En cada punto de la curva C donde r''(s)≠0 están definidos los tres vectores siguientes
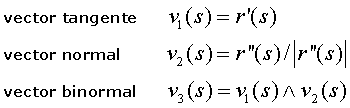
El sistema de vectores anterior es ortonormal y se denomina triedro móvil de Frenet. Asociados a cada uno de los vectores del triedro móvil tenemos una recta y un plano:
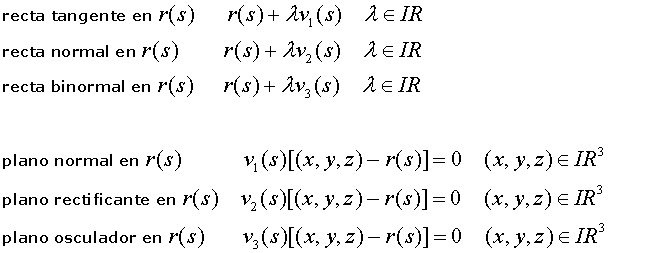
El triedro móvil se encuentra definido sólo en aquellos puntos en los que r''(s)≠0. Si este vector es nulo en un conjunto discreto de puntos de la curva, entonces la curva queda dividida por estos puntos en arcos en los que sí se tendrá triedro móvil. Las curvas para las que r''(s)≠0 en un intervalo serán, en dicho intervalo, un segmento de recta.
Definición Se denomina curvatura de una curva C en un punto r(s) siendo s un parámetro longitud de arco a
![]()
Intuitivamente la curvatura mide lo que se le falta a la curva para ser una recta en cada punto.
Definición Se denomina torsión de una curva C en un punto r(s) siendo s un parámetro longitud de arco a
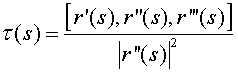
Intuitivamente, la torsión mide lo que le falta a la curva para estar contenida en un plano, es decir, para ser una curva plana.
Para un parámetro arbitrario t se tiene
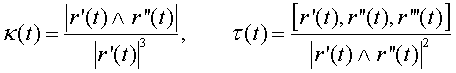
Teorema Es condición necesaria y suficiente para que una curva sea una recta que la curvatura sea idénticamente nula.
Teorema Es condición necesaria y suficiente para que una curva no rectilínea sea plana que la torsión sea idénticamente nula.