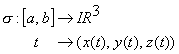
Integrales sobre curvas

Integral de trayectoria

Definición La integral de trayectoria, o integral de f(x,y,z) a lo largo de la trayectoria s, está definida cuando

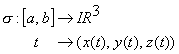
es de clase C¹ y la función f es continua sobre s([a,b]). Definimos esta integral como

Aplicación la integral de trayectoria de la función idénticamente 1 da la longitud de la trayectoria:

El valor promedio de una función f sobre una curva se define como

Integral de línea

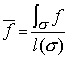
Definición Sea F un campo vectorial 

continuo sobre la trayectoria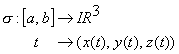  

de clase C¹ . Definimos la integral de línea de F a lo largo  s como

La integral de línea de un campo vectorial F sobre una curva s se puede expresar como la integral de trayectoria sobre dicha curva de la componente tangencial de F como vemos en la siguiente fórmula

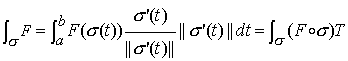
Aplicaión Si F representa un campo de fuerzas en el espacio, su integral de linea define el trabajo que realiza sobre una partícula de prueba a lo largo de la trayectoria s.

Teorema  Si s₁ y s₂ son dos parametrizaciones C¹ de una misma curva que están relacionadas por un cambio admisible de parámetro y

f es un campo escalar continuo sobre la curva :

Para  F campo vectorial continuo sobre la curva

1.- si el cambio de parámetro conserva la orientación entonces

2.- si el cambio de parámetro cambia la orientación entonces

Teorema de campos conservativos Sea F un campo vectorial de clase C¹ definido en IR³ salvo, quizás, en un número finito de puntos. Las siguientes condiciones sobre F son equivalentes

• Para cualquier curva cerrada simple orientada C,   = 0
• Para cualesquiera dos curvas simples orientadas C₁ y C₂ que tengan los mismos extremos
• F es el gradiente de algún campo escalar f, es decir  
•