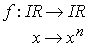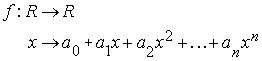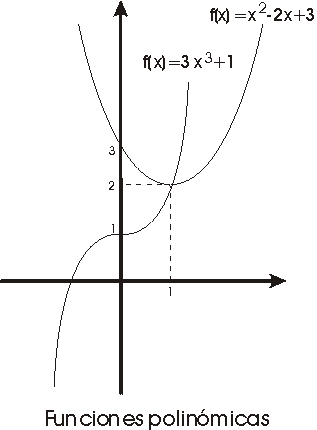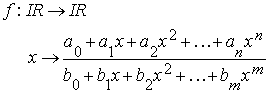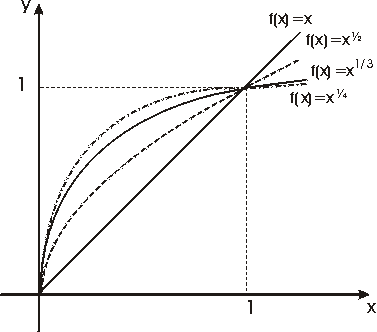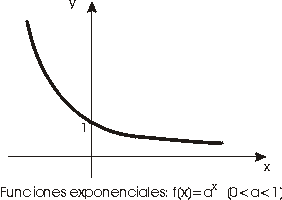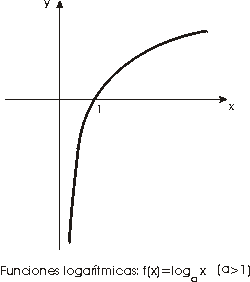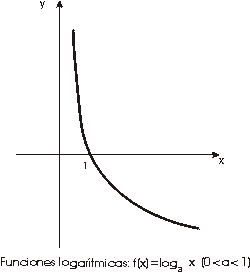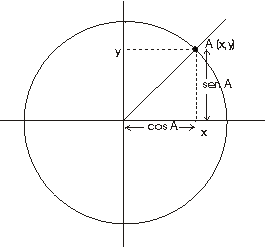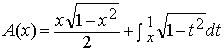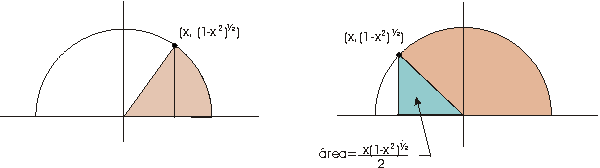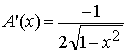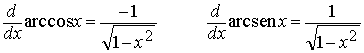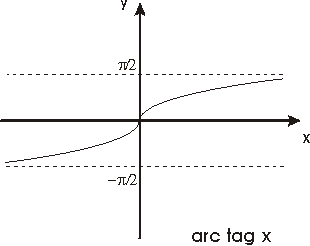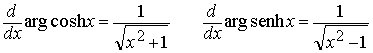Potencias de base real y exponente
entero.
Cuando el exponente es un entero positivo recuperamos la definición
del apartado anterior.
Para los enteros negativos -n se define
x-n=(1/x)n=(x-1)n
y finalmente si n=0 convendremos que x0=1.
Tenemos pues
Definición.- Para cualquier
nÎ
Z se define la función potencia n-ésima como la función
que a cada xÎ IR le asigna xn.
Las propiedades 1, 2 y 3 que vimos
para las potencias de exponente natural se generalizan sin dificultad a
este caso. Para exponente negativo –n tenemos:
4’ Si 0<x<y
entonces 0<y-n<x-n.
Es
decir la potencia de exponente negativo es una función estrictamente
decreciente en (0,¥
).
5’ La función potencia de
exponente negativo esta acotada inferiormente
en (0,¥ ). Más
concretamente se tiene
6’ Sin embargo, no
está acotada superiormente en
dicho intervalo puesto que
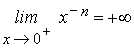
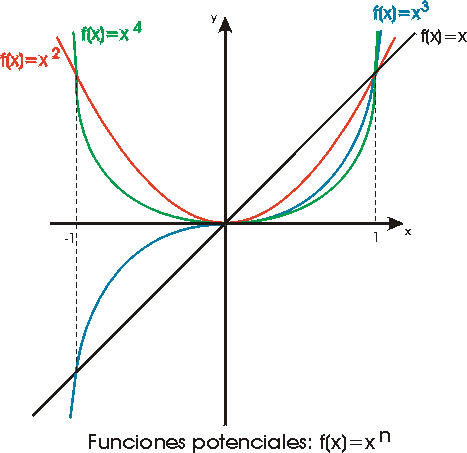
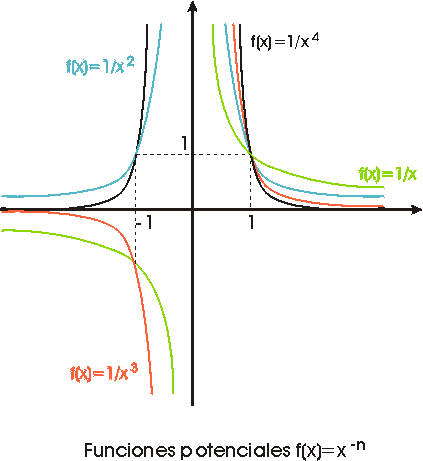
Las siguientes gráficas muestran algunas funciones potencia
con exponente negativo; nótese que en el 0 no están definidas.
Raíces de índice natural
de números reales positivos.
Definición.- Dado un número
real positivo x y un número natural n, se dice que
otro número real
y
es la raíz n-ésima
de x si se verifica
yn=x.
Teorema.- Todo número real
positivo posee una única raíz n-ésima positiva.
Si n es par los números reales positivos tienen
además una raíz n-ésima negativa.
En la figura se muestran las gráficas de las funciones raiz segunda,
tercera y cuarta positivas.
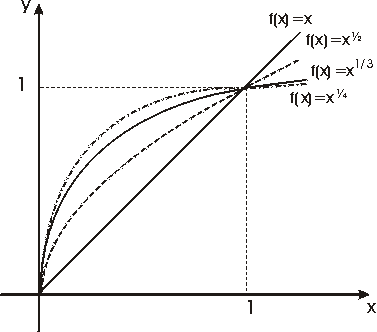
Potencias de base real y exponente
racional.
Definición.- Sea x>0
un número real positivo y r=p/q un número
racional con q>0 y p/q
irreducible, se define xr como la
raíz
q-ésima de xp(nótese
que xpes un número real positivo
y por tanto su raíz q-ésima está definida).
Si q es impar entonces xr
toma un único valor (positivo), si q es par entonces la raíz
toma dos valores reales de signos opuestos. Esto nos lleva a la siguiente
definición:
Definición.- La aplicación
que a cada número real x>0 le hace corresponder xr
(>0)
tomando para todo x la misma determinación positiva en caso
de que q sea par se denomina función potencia de exponente
r.
Las propiedades 1,2 y 3 de las potencias
con exponente entero se pueden generalizar al caso racional. Además
tenemos:
4’’ si 0<x<y
entonces 0<xr<yr
si r>0 y 0<yr<xr
si r<0. Es decir las potencias de
exponente
racional positivo son funciones
estrictamente
crecientes mientras que las de exponente
racional negativo son estrictamente decrecientes en
(0,+¥
).
5’’ Las funciones potencia de exponente
racional positivo no están
acotadas
superiormente en
(0,+¥
), de hecho si r>0
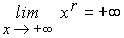
Las funciones potencia de exponente racional
negativo están acotadas inferiormente
por ser positivas en (0,+¥
), más concretamente
si r<0
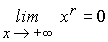
6’’ Las potencias de exponente
racional positivo están acotadas
inferiormente en (0,+¥
) y se tiene para r>0
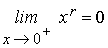
Las potencias de exponente racional negativono
están acotadas superiormente
en dicho intervalo pues si r<0
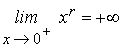 7’’ La propiedad siguiente nos
permite comparar dos funciones potencias con exponentes racionales distintos:
7’’ La propiedad siguiente nos
permite comparar dos funciones potencias con exponentes racionales distintos:
si r < s entonces xr<
xs cuando x>1
y
xs < xr cuando 0<x<1.
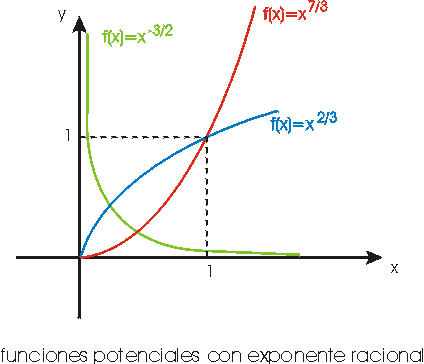
Potencias de base real positiva y
exponente real.
Recordemos que todo número real viene definido por un par sucesiones
de números racionales monótonamente convergentes, cuyo límite
común es precisamente el número real en cuestión.
Utilizando este hecho definimos la potencia de exponente real usando la
potencia de exponente racional que hemos definido en el apartado anterior.
Definición.- Dado un par
de números reales x>0 y a>0
, si rn y sn
son
las sucesiones de números racionales positivos que definen
a
entonces
se define la potencia
a de x como
el número real
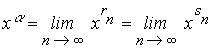
Cuando el exponente sea real negativo a<0,
se tiene xa =(x-a
) -1
.
Para
a=0
convendremos que
x0=1.
Definición.- La función
potencia de base real positiva y exponente real a se
define como la aplicación que a cada número real
x>0
le hace corresponder el número real xa
A continuación recogemos las propiedades
de
esta función que generalizan las vistas para las otras funciones
potencia:
-
xa ya=(xy)a
para
cualesquiera x,y Î IR.
-
xa xb=xa+b
cualesquiera
que sean los números reales a
y
b
.
-
(xa )b=xa
b
cualesquiera que sean los números reales a
y
b
.
-
Si 0<x<y se tiene: 0
< xa <
ya para
a>0
y 0 < ya
<
xa para
a<0.
Es decir las funciones potencia con exponente
real positivo son estrictamente crecientes mientras que las
de exponente negativo son estrictamente
decrecientes y ambas positivas en el intervalo (0,+¥
).
-
Las funciones potencia de exponente real no
están acotadas superiormente
en (0,+¥ ) mientras
que si lo están inferiormente.
De hecho se tiene
-
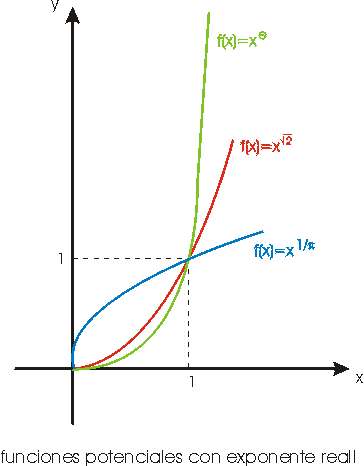
Si a< b entonces:
xa
<
xb cuando
x
> 1 y xb
<
xa cuando
0
< x < 1
La función exponencial
Definición.-Sea a
un número real positivo. La aplicación que a cada número
real x le asigna la potencia ax
se denomina función exponencial de
base a.
Las figuras siguientes muestran funciones exponenciales en las que se
observan las propiedades que se detallan a continuación.
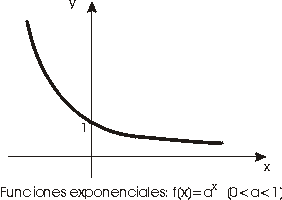
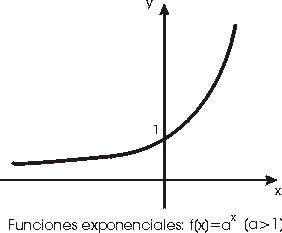
Propiedades:
-
ax >0 para todo xÎ
IR .
-
La función exponencial de base a>1
es estrictamente creciente, mientras
que la de base a<1 es estrictamente
decreciente.
-
La función exponencial de base mayor que
1 no está acotada superiormente aunque silo
está inferiormente IR. Se tiene
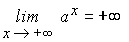
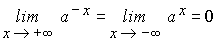
-
Si 0<a<1 la función
exponencial de base a no está
acotada
superiormente aunque si
lo esta inferiormente en IR. De hecho
se verifica:
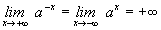
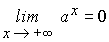
-
Si 0<a<b entonces: ax <
bx si
x>0 y bx
<
ax si x<0.
-
Cualquiera que sea el número real positivo y existe un único
número real x tal que ax=y.
El número x se llama logaritmo
en base a de y y se representa
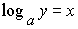
Esta última propiedad nos sirve para definir una nueva función,
inversa de la anterior en el sentido de que la composición de ambas
da la función identidad.
La función logarítmica
Definición.-Sea a
un número real positivo. La aplicación que a cada número
real x>0 le asigna
loga x
(que es único) se denomina función logarítmica en
base a.
Las propiedades de está función
se deducen inmediatamente de las de la función exponencial:
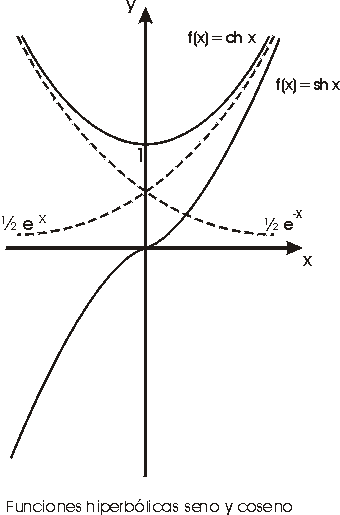
Las funciones hiperbólicas.
Definición.- Llamaremos función
coseno hiperbólico y función seno hiperbólico a las
aplicaciones de IR en sí mismo, que representaremos por cosh
x y senh x respectivamente, definidas por las siguientes expresiones
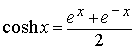
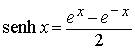
A partir del seno y coseno hiperbólicos se pueden definir el
resto de las funciones hiperbólicas: tangente,
cotangente, secante y cosecante hiperbólicas, como

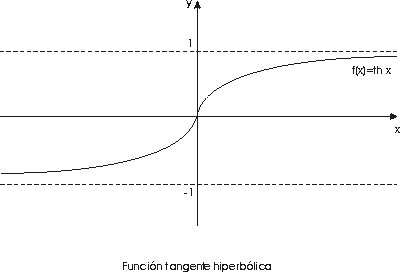
A partir de las definiciones se deducen las siguientes
igualdades
cosh (-x)= cosh x;
senh (-x)= -senh x;
th(-x)=-th x.
cosh2 x-senh2 x=1;
1-th2 x=1/cosh2 x;
cosh (x+y)=cosh x chos y+ senh x senh y;
cosh 2x= cosh2 x +senh2 x;
cosh (x-y)=cosh x chos y- senh x senh y;
senh (x+y)=senh x chos y+cosh x senh y;
senh 2x=2 senh x cosh x;
senh (x-y)=senh x chos y- cosh x senh y;
th (x+y)= (th x+ th y)/(1+th x thy);
th(x-y)=(th x-th y)/(1- th x th y);
Las funciones trigonométricas
circulares.
Las funciones trigonométricas básicas son el seno y el
coseno. El resto de las funciones trigonométricas se obtiene a partir
de ellas. Comenzamos con una definición informal. Para ello necesitamos
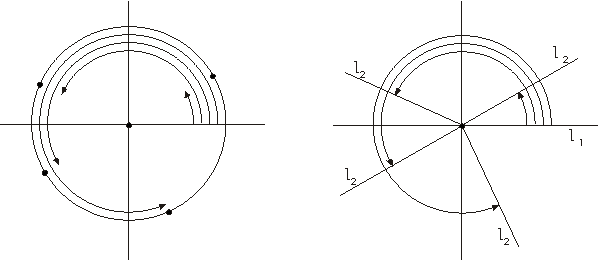
el concepto de ángulo dirigido.
Un ángulo dirigido puede
ser considerado como un par de semirrectas
(l1,l2)
con el mismo punto inicial.
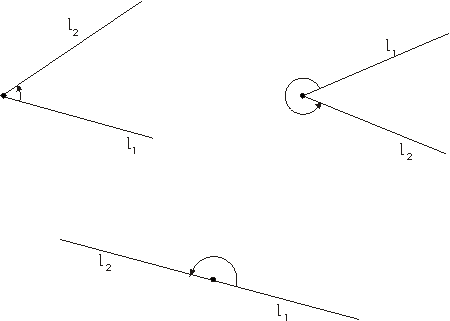
Si para l1 elegimos siempre la mitad positiva del
eje horizontal, un ángulo dirigido vendrá descrito mediante
la segunda semirrecta. Puesto que cada semirrecta corta al círculo
unidad exactamente una vez, un ángulo dirigido
queda descrito, aún más sencillamente, mediante
un punto sobre el círculo unidad, es decir un punto (x,y)
tal que
x2+y2=1.
Entonces el seno del ángulo
se define como la ordenada
y del punto que lo representa y el
coseno como la abcisa x, según se representa en
la figura siguiente:
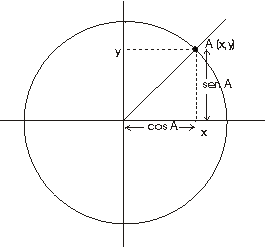
Sin embargo queremos definir el seno y el coseno
de cualquier número real x .
El procedimiento usual es asociar un ángulo a cada número.
Esta asociación se lleva a cabo del modo siguiente: dado un
número real cualquiera x, elíjase un punto P sobre
el círculo unidad tal que x sea la longitud del arco de círculo
que empieza en (1,0) y que se dirige hacia P en sentido contrario al de
las agujas de un reloj.
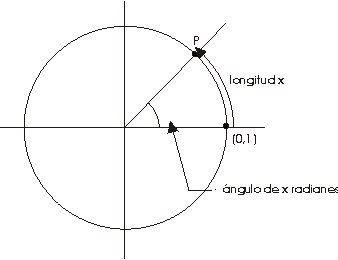
El ángulo así construido determinado por P se denomina
ángulo
de x radianes. Al ser
2p la
longitud total del círculo, el ángulo de x radianes
y el ángulo de 2p +x radianes
son idénticos.
Se puede definir ahora el seno de
xcomo
el seno del ángulo de x radianes.
La definición anterior depende del concepto de longitud de una
curva. Para evitar esto, formularemos de nuevo la definición en
términos de áreas
(que puede ser tratadas mediante la integral).
Supongamos ahora que x es la longitud del arco del círculo
unidad desde (1,0) hasta P; este arco contiene así
x/2p
de
la longitud total (2p )
de
la circunferencia del círculo unidad.
Designemos por S el sector del círculo determinado por el ángulo
definido por P (ver la figura).
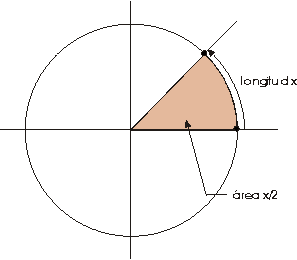
El área de este sector ha de ser x/2p
veces
el área del círculo unidad, la cual damos por supuesto que
es p .
Entonces el área de S es (x/2p
)p =x/2.
Podemos definir ahora el coseno de x y el seno de x,
que denotaremos por cos x y sen
x, respectivamente, como
las coordenadas del punto P que determina un sector de área x/2
en
el círculo unidad.
Para la definición rigurosa comenzamos con la definición
de p como dos veces el área del semicírculo
unidad:
Definición.-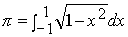
Definamos ahora A(x) para -1 £
x £ 1 como el área del sector
limitado por el círculo unidad, el eje horizontal y la semirrecta
que pasa por el origen y el punto (x,(1-x2)1/2)
sobre
el círculo unidad .
Definición.- Si -1 £
x £ 1, entonces
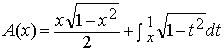
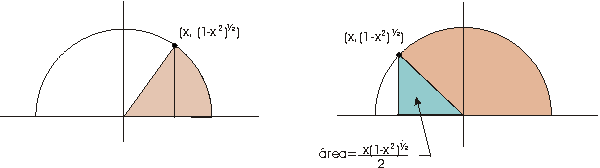
Obsérvese que A(x) es derivable en -1 £
x £ 1 y su derivada es
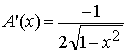
Para 0 £ x £p
queremos
definir cos x y sen x como las coordenadas de un punto P,
(cos x, sen x), sobre el círculo unidad que determina
un sector cuya área es x/2. En otros términos:
Definición.- Si0 £
x £p, entonces cos x es el
único número en [-1, 1] tal que
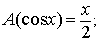
y
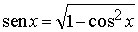
Para saber que existe un número y que satisface A(y)=x/2,
utilizamos el hecho de que A es continua y toma los valores 0 y
p
/2 (teorema de los valores intermedios).
Esta definición se extiende primero al intervalo [-p
, 0 ) de la forma siguiente:
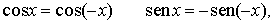
Por último, la definición de
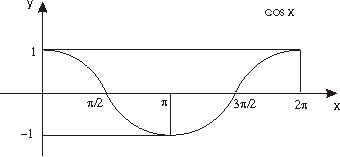
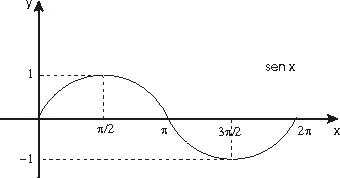
las funciones seno y coseno se extiende a toda la recta real de forma periódica.
Las figuras siguientes muestran esta extensión.


Teorema.- Las funciones seno y coseno
son continuas en IR y admiten derivada en
todo punto verificándose que
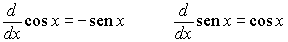
Además, son funciones acotadas
puesto que verifican las siguientes igualdades:
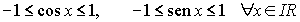
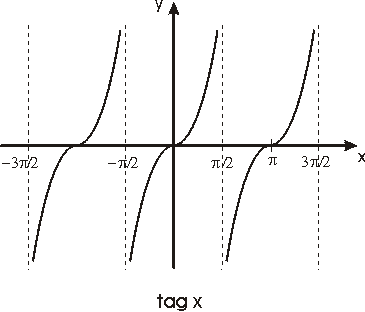
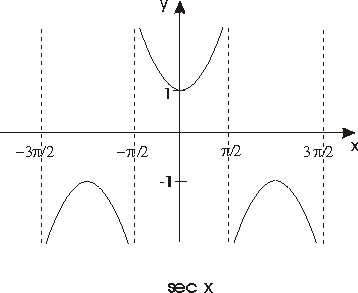
Definición.- El resto de
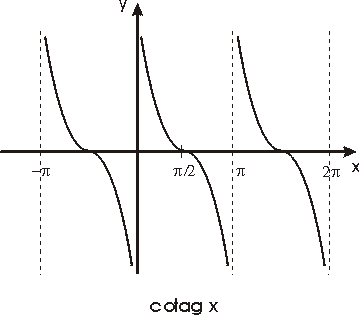
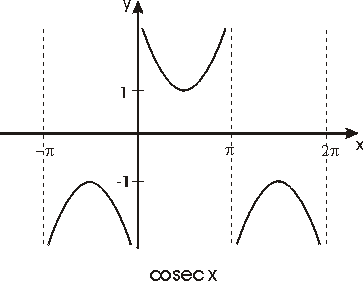
las funciones trigonométricas se definen como sigue:
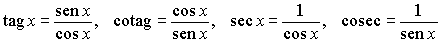
Véanse las gráficas de estas funciones en las figuras
siguientes
Propiedades de
las funciones trigonométricas.
cos2 x + sen2 x =1,
cos(x+y)=cos x cos y -
sen x sen y,
cos 2x= cos2 x -
sen2x
cos(x- y)= cos x cos y
+ sen x sen y,
sen (x+y)=sen x cos y + cos x sen y,
sen 2x= 2cos x sen y
sen (x- y)=sen x cos y-
cos x sen y
Las funciones trigonométricas
inversas.
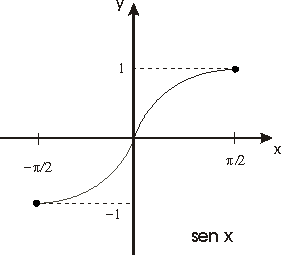
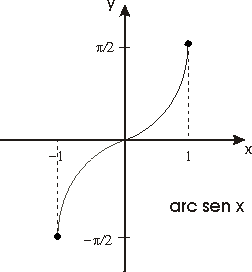
La función f(x)=sen x,
definida en el intervalo cerrado [-p /2,p
/2], es continua, estrictamente creciente y transforma dicho intervalo
en el [-1, 1]. Esta función es pues un homeomorfismo del primer
intervalo sobre el segundo y su función inversa que denotaremos
por
f
-1(x)=arc sen x
estará definida de [-1, 1] siendo
también continua y estrictamente creciente.
Es inmediato comprobar que arc sen (-
x)=- arc sen x para todo x en [-1,
1].
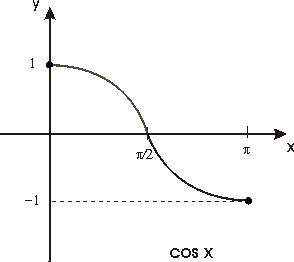
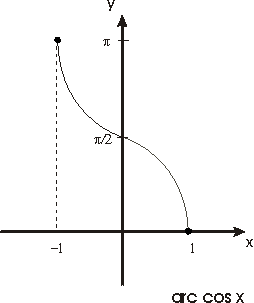
La función f(x)=cos x,
definida en el intervalo cerrado [0, p ], es
continua, estrictamente decreciente y transforma dicho intervalo en el
[-1, 1]. Esta función es pues un homeomorfismo del primer intervalo
sobre el segundo y su función inversa que denotaremos por
f -1(x)=arc cos x
estará definida de [-1, 1] siendo
también continua y estrictamente decreciente.
Nòtese que en ambos casos las funciones seno y coseno no se han
considerado en toda la recta real puesto que no en ella no son inyectivas
y por lo tanto su función inversa no estaría definida.
Teorema.- Las funciones trigonométricas
inversas arc cos x y arc sen x definidas en el intervalo
[-1,1] son derivables en todos los
puntos de (-1, 1) y se tiene
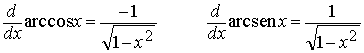
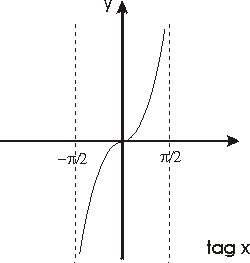
La función f(x)=tag x,
definida en el intervalo (-p /2,p
/2), es continua, estrictamente creciente y transforma dicho intervalo
en IR puesto que
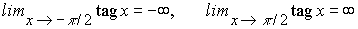
Esta función es pues un homeomorfismo del primer intervalo sobre
toda la recta real y su función inversa
f -1(x)=arc tag x
que estará definida en IR,
es también continua y estrictamente creciente.
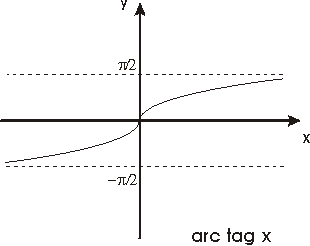
Además arc tag x es derivable en todo punto y su derivada
viene dada por
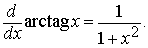
Las funciones trigonométricas inversas verifican las siguientes
igualdades
arc cos x + arc cos (-x) = p ,
arc cos x + arc sen x = p /2,
arc tag x = -arc tag (-x).
El resto de las funciones trigonométricas
inversas se consiguen de forma similar aunque es usual considerar
la función cotangente definida en (0,p
), la función secante definida en [0, p
]-{p /2} y la función cosecante en el
intervalo [-p /2,p
/2]-{0} (donde son inyectivas) para definir sus inversas que entonces verificarán
las siguientes igualdades:
-
arc cotag x = p /2 -
arc tag x,
-
arc sec x = arc cos (1/x),
-
arc cosec x = arc sen (1/x).
Las funciones hiperbólicas
inversas.
La función f(x)=senh x,
definida en toda la recta real, es continua y estrictamente creciente.
Además se tiene
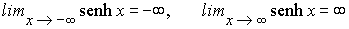
Luego esta función es un homeomorfismo de IR en IR, su función
inversa
f -1(x)=arg sh x
(argumento del seno hiperbólico) es también continua
y estrictamente creciente en IR.
La función arg sh x se puede expresar utilizando la función
logaritmo como
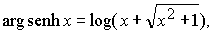
para demostrar esto basta observar que
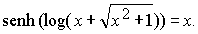
La función cosh x es
continua y estrictamente creciente en el intervalo [0, ¥
) y se tiene
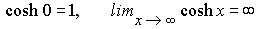
Luego esta función es un homeomorfismo del citado intervalo sobre
[1, ¥ ). Su función
inversa
f -1(x)=arg cosh x
(argumento del coseno hiperbólico) es también continua
y estrictamente creciente definida en [1,¥
) .
De igual forma que arg senh x , se puede expresar mediante el logaritmo
como
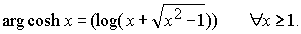
Si tomamos ahora la función cosh x en la semirecta (-¥
, 0], aquí dicha función es continua y estrictamente decreciente
y resulta ser un homeomorfismo de dicho intervalo en [1, ¥
) . Por lo tanto tenemos definida la función inversa que se expresa
utilizando el logaritmo como
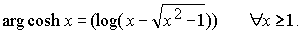
Como podemos observar tenemos dos valores de arg cosh para cada
x
en la semirecta [1, ¥).
Esto indica que la función arg cosh x es multivaluada:
cada una de las funciones univaluadas arg cosh x definidas anteriormente
se conoce como una determinación o rama de la función arg
cosh x multivaluada.
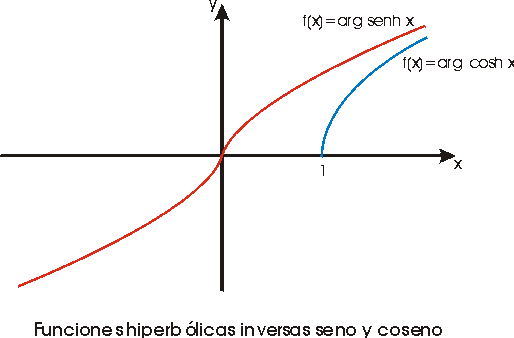
Teorema.- Las funciones hiperbólicas
inversas son derivables y sus derivadas
vienen dadas por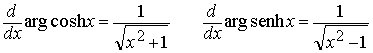
Por último para la función th x, definida en toda
la recta real y estrictamente creciente en ella, se tiene definida su inversa
en el intervalo (-1, 1), puesto que
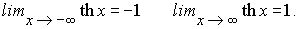
Dicha función inversa, arg
th x, está definida, es continua y estrictamente
creciente en el intervalo (-1, 1) y se expresa utilizando el logaritmo
como
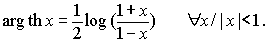
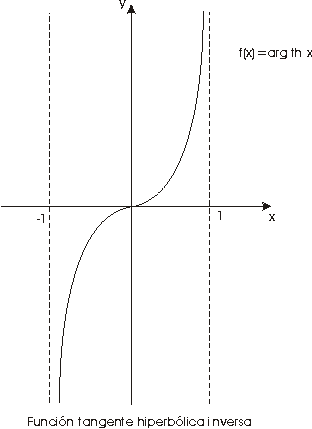
La derivada de esta función
viene dada por
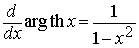
El resto de las funciones hiperbólicas
inversas se definen análogamente.
![]()