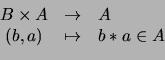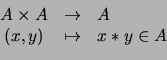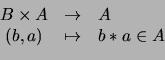Siguiente: Estructuras algebraicas Subir: OPERACIONES Y ESTRUCTURAS ALGEBRAICAS Anterior:
OPERACIONES Y ESTRUCTURAS ALGEBRAICAS
En primer lugar introducimos el concepto de operación binaria,
tanto interna como externa, si bien nos centraremos en el primer
caso, puesto que el ejemplo más interesante de operación externa
tiene que ver con espacios vectoriales, que se estudiarán con
detalle en la correspondiente asignatura del Plan de Estudios
(Álgebra Lineal).
Definición 1.1

- i)
- Una operación interna `
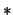 ' en un conjunto
' en un conjunto 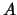 es una aplicación
es una aplicación
- ii)
- Una operación externa `
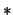 ' en
' en 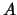 con operadores en
con operadores en 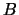 (por la izquierda) es una aplicación
(por la izquierda) es una aplicación
En lo que sigue supondremos que `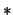 ' es una operación interna en
' es una operación interna en 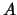 .
En ese caso, un subconjunto
.
En ese caso, un subconjunto
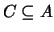 se dice que es cerrado con respecto
a dicha operación si se verifica que
es decir, al hacer operaciones con elementos de
se dice que es cerrado con respecto
a dicha operación si se verifica que
es decir, al hacer operaciones con elementos de 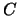 no nos salimos del
conjunto
no nos salimos del
conjunto 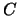 . Por otra parte, una operación interna puede cumplir o no
(entre otras) las siguientes propiedades:
. Por otra parte, una operación interna puede cumplir o no
(entre otras) las siguientes propiedades:
- Asociativa:
-
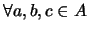 ,
,
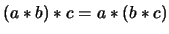 .
.
- Conmutativa:
-
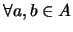 ,
,
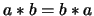 .
.
- Elemento Neutro:
-
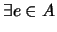 ,
,
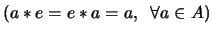 .
.
- Elemento Inverso:
- Suponiendo que existe elemento neutro
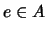 , entonces
se dice que un elemento
, entonces
se dice que un elemento 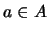 tiene inverso (u opuesto) si
tiene inverso (u opuesto) si
- Distributiva:
- Dadas dos operaciones internas `
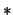 ' y `
' y `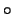 '
en
'
en 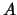 , se dice que `
, se dice que `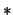 ' es distributiva respecto de `
' es distributiva respecto de `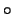 ' si
' si
- Otras:
- no se verán con mucho detalle, pues tienen que ver principalmente con
Retículos y Álgebras de Boole, que es un tema muy específico de Informática.
Hacemos notar que el elemento neutro, en caso de existir, es único,
y lo mismo ocurre con el elemento inverso 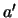 de un elemento dado
de un elemento dado 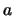 .
.
Siguiente: Estructuras algebraicas Subir: OPERACIONES Y ESTRUCTURAS ALGEBRAICAS Anterior:
OPERACIONES Y ESTRUCTURAS ALGEBRAICAS
Jose Ignacio Farran Martin
2003-07-16
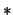 ' en un conjunto
' en un conjunto 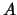 es una aplicación
es una aplicación
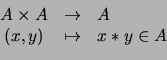
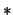 ' en
' en 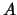 con operadores en
con operadores en 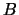 (por la izquierda) es una aplicación
(por la izquierda) es una aplicación