---

En lo que sigue trabajaremos siempre en el espacio vectorial IRⁿ sobre el cuerpo IR. Nos fijaremos especialmente en los casos n = 2 y n= 3.

---

 

Puntos y vectores libres

Llamaremos punto del espacio IRⁿ a cualquiera de sus elementos (x₁, x₂,...,x_n), es decir identificaremos puntos y vectores.

Cuando pensemos en los elementos de IRⁿ como puntos les denotaremos con letras mayusculas P, Q,... mientras que si los vemos sólo como elementos del espacio vectorial seguiremos denotándoles por u, v,... Las expresiones del tipo

                                P+u, P+Q, a P donde aÎ IR, u=P, ....

tiene sentido puesto que u,P,Q pertenecen al mismo espacio vectorial: por ejemplo si P=(1,3), Q=(5,2) y u=(4,1) entonces P+Q es el punto (6,5) y u+P es el punto (5,4) (véase la figura siguiente).
 

 
 

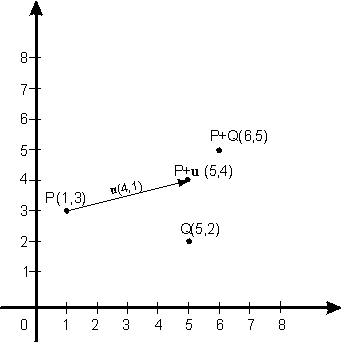
El vector 0 como punto se denomina origen y se denotará por O.

Dados dos puntos A y B de IRⁿ se les asigna el vector B-A que llamaremos vector libre con origen en A y extremo en B y designaremos por vect  (AB). Claramente dos vectores libres pueden ser iguales aunque los puntos que definen sus extremos sean diferentes. De hecho un vector libre u se puede interpretar como un conjunto de pares de puntos cuya diferencia es igual a u. A cada par de puntos se le denomina representante del vector libre (de hecho un vector libre u es una clase de equivalencia para la relación entre puntos A r B • B-A=u ).

Cuando queramos interpretar un vector como vector libre podremos elegir su origen de forma arbitraria pero entonces el extremo queda unívocamente determinado:

Resultado: dado un vector uÎIRⁿ y un punto AÎ IRⁿ cualquiera entonces existe un único punto B tal que u=vect(AB)

Ejemplo:

1  Sea u=(4,3),

• Si elegimos A=(1,-2) entonces B=(5,1)
• Si elegimos A=(1,3) entonces B=(7,4)

    (Véase la figura)
2  Sea u=(5,0,-1)

• Si A=(0,-1,7) entonces B=(5,-1,6)
• Si A=(11,2,1) entonces B=(16,2,0)

 

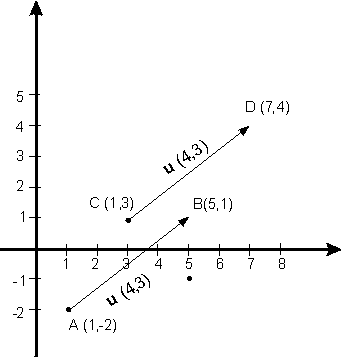
Resultado: para cualesquiera tres puntos A,B,C se tiene  vect(AB)+vect(BC)=vect(AC)
 

Distancia y longitud en IRⁿ

Si A=( a_1, a₂ ,..., a_n) y B=( b₁, b₂ ,..., b_n) son dos puntos de IRⁿ la distancia entre A y B se define como el número real positivo

                    d(A,B)=((b₁- a₁)²+(b₂ - a₂)²+...+(b_n - a_n)²) ^{1/ 2}
 

Propiedades de la distancia:

Para cualesquiera puntos A y B de IRⁿ

• d(A,B)=d(B,A),
• d(A,B)=0 sí y sólo si A=B,
• d(A,B)=d(O,B-A).

El número d(A,B) se denomina longitud o módulo del vector libre u=vect(AB) y se denota por | u |
 

Propiedades del módulo:

Para cualesquiera vectores u y v de IRⁿ

1. | u |=(u₁²+u₂²+...+u_n²) ^{1/ 2}
2. | u |=0 sí y sólo si u=0
3. | a u |=| a |.| u | con aÎ IR
4. |u+v | £ | u |+| v |

 

Dos vectores u y v de IRⁿ se dicen que son paralelos (u || v) si uno es un múltiplo escalar del otro, es decir u Î< v >
 

Propiedades del paralelismo:

Para cualesquiera vectores u , v, w de IRⁿ

1. u || u
2. si u || v entonces v || u
3. si u || v  y  v || w entonces u || w
4. El conjunto de vectores paralelos a v es < v >. En particular si dos vectores u y w son paralelos a v entonces cualquier combinación lineal suya es paralela a v .
5. Si u ¹ 0 entonces u || v sí y sólo si < u > = < v >

 

 
 

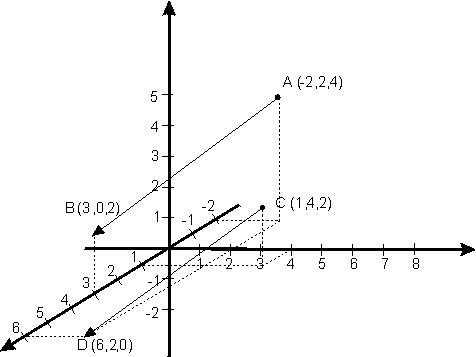
Variedad afín

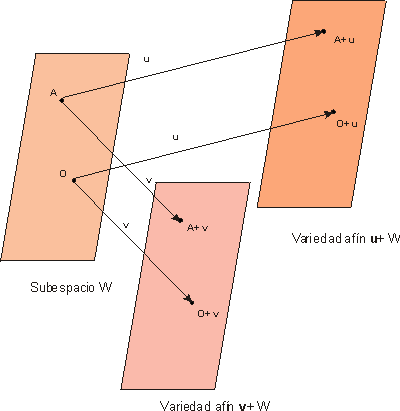
Un subconjunto V del espacio vectorial IRⁿ es una variedad afín si V=u+W donde W es un subespacio vectorial, es decir todo elemento de V se escribe como suma de u más un vector w ÎW. W se denomina subespacio director de la variedad afin.

La dimensión de la variedad afín V se define como la dimensión de su subespacio director W: dim V=dim W.

Ejemplo:

    En la figura siguiente obtenemos variedades afines de dimensión 2 (planos afines) a partir del subespacio W (contiene el origen)


 
 
 


Producto escalar real y espacio real Euclídeo

Dados dos vectores cualesquiera de IRⁿ u=( u_1, u₂ ,..., u_n) y v=( v₁, v₂ ,..., v_n) se define su producto escalar u.v como

                                                u.v= u₁ v₁ + u₂ v₂ +...+u_n v_n

Propiedades del producto escalar:

Dados dos vectores cualesquiera u y v de IRⁿ

1. u.v=v.u
2. u.(v+w)=(u.v)+(u.w)
3. a (u.v)= (au) v= u (av) con aÎ IR


Claramente se tiene que u.u =| u |²  y  u.u =0 sí y sólo si  u = 0.

El producto escalar real también se conoce como producto interno real y se puede generalizar a cualquier espacio vectorial. Un espacio vectorial en el que se ha definido un producto interno real se denomina espacio Euclídeo real. El producto interno permite definir el concepto de distancia y módulo o norma de cualquier vector en el correspondiente espacio Euclídeo.

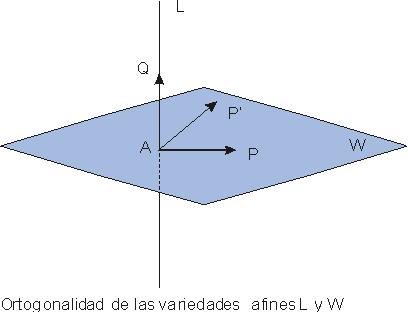
Perpendicularidad u ortogonalidad

Dos vectores u y v de IRⁿ se dicen que son ortogonales o perpendiculares (u ^ v) si u.v = 0, es decir su producto escalar es nulo.

Dos variedades afines V₁ y V₂ que se cortan en un punto A son perpendiculares u ortogonales en dicho punto si
 

AP₁  ^  AP₂ para cualesquiera P₁ ÎV₁ y P₂ÎV₂

 



Teorema de Pitágoras

Dados dos vectores u y v de IRⁿ ortogonales se verifica

                        | u+v | ² =| u | ² + | v | ²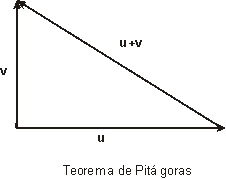 
Generalización

Dados k vectores de IRⁿ , v₁, v₂,...,v_k , ortogonales, se tiene

            | v₁+ v₂ + ... +v_k | ² = | v₁ | ² + | v₂ | ² + ...+ | v_k | ²
 

El producto interno o escalar permite definir ángulos en el espacio afín.

Dados dos vectores, u y v, se dice que son ortonormales si son ortogonales (u.v = 0) y ambos tienen módulo 1 ( | u |=| v |=1).

Dados dos vectores u y v de IRⁿ se define el ángulo que forman como:

                        ang(u,v) = arc cos (u.v /| u |. | v | )

Claramente el ángulo que forman dos vectores perpendiculares es p /2
 

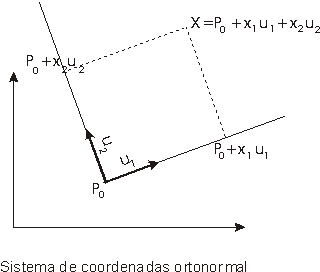
Sistema de coordenadas ortogonal en IRⁿ

Un sistema de coordenadas ortogonal en IRⁿ es una n+1-upla K={ P₀; u₁, u₂,..., u_n } donde P₀ es un punto de IRⁿ y { u₁, u₂,..., u_n } es una base ortogonal de IRⁿ

Si P es un punto de IRⁿ, sus coordenadas en el sistema ortogonal K son x₁ , x₂ ,..., x_n sí y sólo si

            v= vect(P₀P)= x₁ u₁+ x₂ u₂ +...+ x_n u_n .
Además x_i =v.u_i

El sistema se dice que es ortonormal si los vectores u_i son ortonormales.
 


 
 
 
 
 


Transformaciones geométricas en IR³

---

  Movimientos o isometrías   Translaciones    Ecuaciones de un movimiento   Isometrías lineales      Homotecias y semejanzas

---

En lo que sigue denotaremos por E al espacio afín Euclídeo IR³.

Sea f una aplicación de E en sí mismo

                        f: E ® E

Si f es biyectiva decimos que es una transformación geométrica de E.

Dos punto A y B de E tales que f(A) = B se les llama puntos homólogos por la transformación f. En particular, si f (A)=A, entonces se dice que A es un punto doble.

Un subconjunto E´ de E se dice que es invariante o estable por la transformación geométrica f, si f (E´)=E´.
 
 


Movimientos o isometrías del espacio

Un movimiento o isometría es una transformación geométrica que conserva las distancias, es decir, para cualquier par de puntos A y B de E se verifica

d(A,B)=d(f(A), f(B))

Ejemplo:

La transformación geométrica definida por:

f(x, y, z) = (x+1, y+2, z)

es un movimiento, ya que si A = (x₁, y₁, z₁) y B = (x₂, y₂, z₂) son dos puntos de E, se tiene:

d(A,B)=

Por otro lado

d(f(A), f(B)) = 

= d (A, B)

luego ambas distancias coinciden.

Esta transformación no  tiene ningún punto doble, puesto que si  f(P)=P

f(P) =(x+1, y+2, z)=(x, y, z) = P

entonces las coordenadas de P, (x,y,z), deberían verificar el sistema de ecuaciones



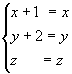
que no admite solución. Sin embargo, el plano de ecuación general  z=0 es invariante por f, ya que cualquier punto P= (x, y, 0) del plano se transforma en
f (P) = (x+1, y+2, 0) que es también  un punto de dicho plano .
 


Translaciones

Se denomina translación de vector u y se denota por T_u a la transformación geométrica que asocia a cada vector x del espacio E el vector x+u, es decir T_u(x)=x+u En términos de puntos T_u(A)=A+u



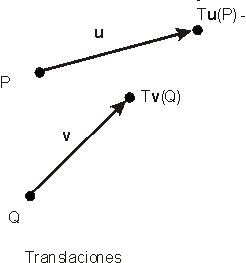
Propiedades de las translaciones:

 
1. Una translación es una isometría (conserva las distancias).
2. La inversa de una translación de vector u es otra translación de vector -u

                                         T_u^-1 = T_-u
3. El producto (composición) de dos translaciones de vectores u y v es otra translación de vector u+v.
                                 T _{u °}T _v = T_u+v

 

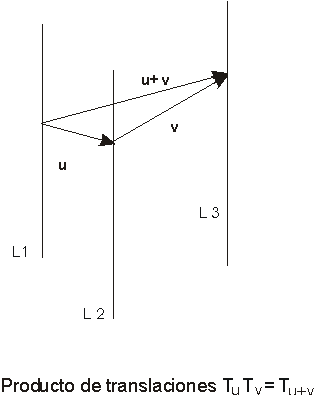
Resultado: Cualquier isometría se puede expresar como el producto de una isometría lineal y una translación.

Veamos como se puede llevar a cabo esta descomposición.

Si f un movimiento de IR³ y f(O)=A entonces f=T_OA S donde S es la transformación que asocia a cada vector x =vect(OX), el vector S(x)=vect(Of(X))-vect(OA), o en términos de puntos S(X)=f(X)-A. S es una isometría lineal.
 

Propiedades de los movimientos

1. Los movimientos transforman rectas en rectas y planos en planos
2. Los movimientos conservan los ángulos
3. Los movimientos conservan el paralelismo.
4. La aplicación inversa de un movimiento es otro movimiento
5. El producto (composición) de dos movimientos es otro movimiento

 
 


Ecuaciones de un movimiento

Sea K={ P₀, u₁, u₂,u₃ } una sistema de referencia ortonormal, f un movimiento y S su isometría lineal asociada. La aplicación lineal S en la base { u₁, u₂, u₃} tendrá una matriz asociada 3 x 3:




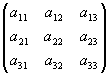
Como cualquier elemento del espacio se escribe como O+u (u=combinación lineal de los u_i) si f(O)=A=(a₁, a₂, a₃) entonces como

                                                                    v=f(O+u)=A+S(u)

tenemos que si (x´,y´,z´)  denotan las coordenadas de v y  (x,y,z)  las de u entonces



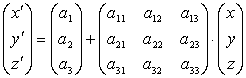
Finalmente la ecuación se puede escribir como



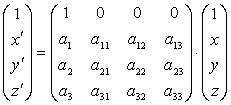
La ecuación de una translación de vector (a₁, a₂, a₃) será


 


Isometrías lineales
 

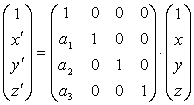
Resultado: Las siguientes proposiciones son equivalentes:

1. f es una isometría y f(0)=0
2. f es una isometría lineal
3. f conserva el producto interno: u.v = f(u).f(v).

 


Caracterización en términos de matrices:

Si S es una aplicación lineal de E en E con matriz asociada A, entonces son equivalentes:

1. S es una isometría
2. Las filas de A son ortonormales
3. Las columnas de A son ortonormales
4. A^t=A^-1
Una matriz que verifica lo anterior se denomina matriz ortonormal
 

Tipos de isometrías lineales


Giro o rotación

Se llama giro de amplitud a y eje de giro e a la transformación G(a , e): E ® E que asocia a cada punto A de E un punto B definido por las siguientes condiciones:

1    El punto B se encuentra en el plano pque pasa por A y es perpendicular al eje de giro e.

2    Los puntos A y B equidistan del eje de giro, es decir, d(Q, A)= d(Q, B) siendo Q el punto de intersección del plano p con el eje e.

3    El diedro de eje e, cuyas caras son los semiplanos que contienen a los puntos A y B vale a
 


 
 

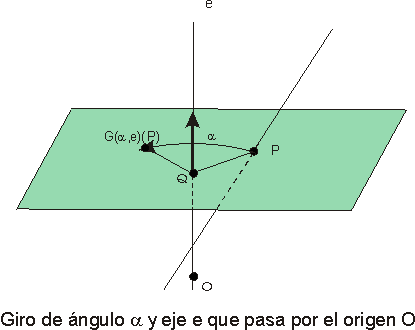
Para determinar el signo del ángulo ang(AQB) es necesario prefijar un sentido positivo de rotación alrededor del eje e. Suponemos elegido como sentido positivo de recorrido del eje e el que va de abajo hacia arriba. Sea A un punto que describe una circunferencia de centro Q; se dice que el sentido de rotación alrededor del eje es positivo cuando supuesto un observador situado en el punto Q y en la dirección positiva del eje, el punto A describe un ángulo en sentido contrario a las agujas del reloj.
 


Simetría respecto de un plano (especular)

Se llama simetría respecto de un plano p a la transformación del espacio E que asocia a cada punto A de E el punto B, tal que el lugar geométrico de los puntos que equidistan del segmento AB es precisamente el plano p , es decir este plano es perpendicular a la recta que une los puntos A y B justamente en el punto medio del segmento AB.
 
 


 
 

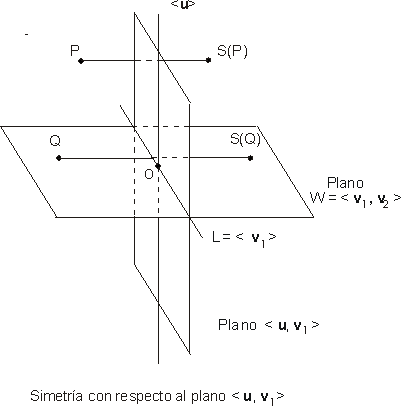
Resultado: Sea S una isometría lineal de E en E entonces:

1. Existe un vector u de E tal que S(u)=±u
2. El subespacio ortogonal a u es S- estable.
 
 
Resultado: Las isometrías lineales de E son de uno de los tres tipos siguientes:
1. Un giro de eje una recta que pasa por el origen de coordenadas
2. Una simetría respecto de un plano que contiene al origen
3. Un giro de ángulo no nulo y eje <u> seguido de una simetría respecto del plano ortogonal al eje del giro.
 

 

Ecuaciones de las isometrías lineales:
 

1. Giro de ángulo a y eje <u>
Si se toma como sistema ortonormal coordenado {O, u, w₁ , w₂} donde <w₁ , w₂> es el plano ortogonal al eje de giro entonces la ecuación del giro es:



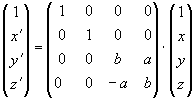
donde a= ± sen a y b= cos a
 

1. Simetría con respecto al plano <w₁ , w₂>
Si se toma como sistema ortonormal coordenado {O, u, w₁ , w₂} donde u es un vector ortonornal al plano de la simetría entonces la ecuación de la simetría es


 

1. Producto de un giro y una simetría

Si se toma como sistema ortonormal coordenado {O, u, w₁ , w₂} donde <u> es el eje de giro y <w₁ , w₂> es el plano ortogonal al eje de giro entonces la ecuación de la isometría es:



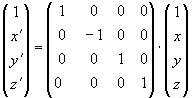
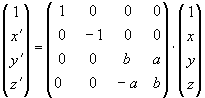
donde a= ± sen a y b= cos a

El tipo de isometría lineal en un sistema de coordenadas arbitrario se puede determinar estudiando los autovalores de su matriz asociada, así tenemos los siguientes casos:
 
 

Tipo de isometría	Descripción	Autovalores reales	Polinomio característico
Giro	Identidad I	1,1,1	-(x-1)3
Giro	Ángulo de giro a=180º	1,-1,-1	-(x-1)(x+1)2
Giro	Ángulode giro a¹ 0º y 180º	1	-(x-1)(x2-2ax+1)  a=cos a
Simetría	Simetría respecto a un plano	1,1,-1	-(x-1)2(x+1)
Giro+simetría	Ángulo del giro a=180º	-1,-1,-1	-(x+1)3
Giro+simetría	Ángulo del giro a¹ 0º y 180º	-1	-(x+1)(x2-2ax+1)  a=cos a


 

Ejemplo
Dada la transformación  f: (x,y,z) ® (x',y',z') de E en E definida por las siguientes ecuaciones:

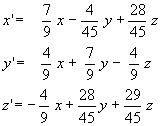
determínese si f es una isometría lineal y en su caso el tipo de dicha isometría.

Solución: claramente f es una aplicación lineal cuya matriz asociada en la base canónica es  A.



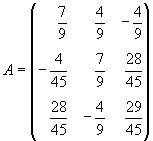
Veamos si A es una matriz ortonormal, i.e.,  AA^t  es la identidad:



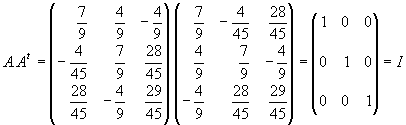
Luego efectivamente f es una isometría lineal. Para ver de que tipo calculamos su polinomio caracteristico



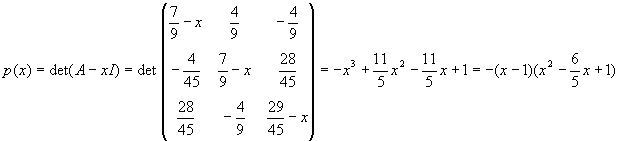
Utilizando la tabla anterior vemos que  f es un giro de ángulo a=arc cos 3/5,   es decir a=53º aproximadamente.
 

Propiedades de los giros:

1    La composición de dos giros con el mismo eje es otro giro de ángulo la suma de los ángulos de partida.

2    El inverso de un giro es otro giro con el mismo eje y de ángulo el opuesto al de partida.
 
 

Simetría respecto de un eje

Una simetría respecto del eje e es un giro de amplitud p y eje de giro e, es decir una simetría respecto de un eje e asocia a cada punto A de E un punto B de forma que la mediatriz del segmento AB coincide con el eje e.

En las simetrías, los puntos homólogos reciben el nombre de puntos simétricos respecto del eje e.
 
 
 


Otras transformaciones del espacio


Homotecias

Se llama homotecia de centro C y razón k a la aplicación, denotada por H(C, k) del espacio afín euclídeo E en sí mismo que asocia a cada punto A de E el punto B que cumple la condición: vect(CB)=k vect(CA)

La homotecia se llama directa si la razón es positiva; en caso contrario, diremos que la homotecia es inversa.
 
 

Las homotecias de razón k, |k|¹1, no son movimientos.
 
 


 
 

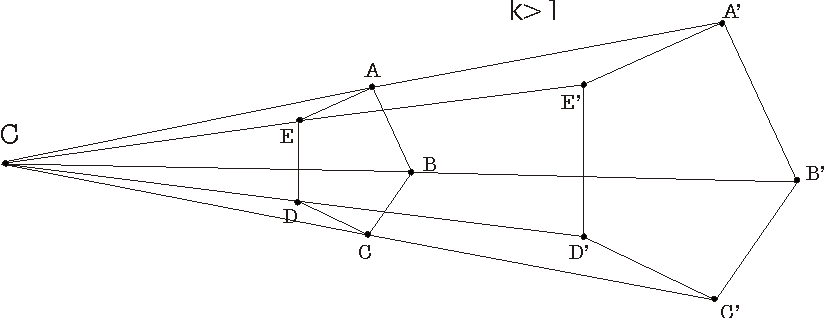
En la figura anterior se muestra el transformado del polígono de vértices A, B, C, D y E mediante una homotecia de razón mayor que 1
 

Ecuaciones de una homotecia

Sea K={O; u₁, u₂, u₃ }un sistema de referencia ortonormal y H(C, k) una homotecia de centro C y razón k.

Si X=(x, y, z) un punto arbitrario del espacio afín tridimensional y sea X´ = (x´, y´, z´ ) el punto transformado de X por la homotecia H(C, k). Se tiene

vect(CX')=k vect(CX) Þ (1-k)vect(OC)+k vect(OX)

o bien

X'=C+k vect(CX)

que es la ecuación vectorial de la homotecia H(C, k).
 
 
 
 


 

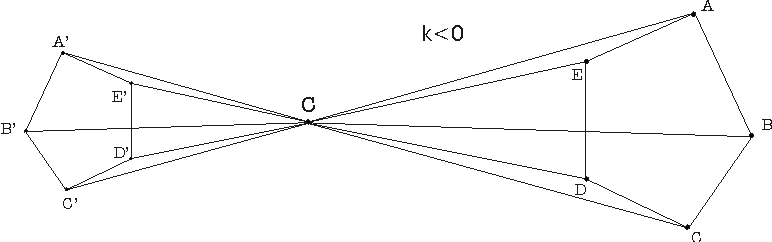
En la figura anterior se muestra el transformado del polígono de vértices A, B, C, D y E mediante una homotecia de razón negativa
 
 

Sustituyendo X´ , C y vect(CX) por sus coordenadas en el sistema de referencia K, se obtiene la ecuación matricial:



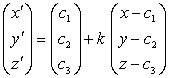
o bien



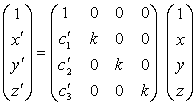
que son las ecuaciones de la homotecia H(C, k) donde




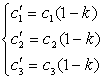
Producto de homotecias

Se llama producto de las homotecias H(C, k) y H' (C' ,k' ) a la aplicación compuesta de ambas aplicaciones: H' (C', k' ) o H(C, k)
 

El producto de dos homotecias del mismo centro C es otra homotecia de centro C, y razón, el producto de las razones, esto es

H' (C, k' ) o H(C, k) = H₁(C, kk' )

El producto de dos homotecias de distinto centro es o bien otra homotecia, cuyo centro está alineado con los centros de las homotecias dadas y de razón el producto de las razones de dichas homotecias.

H´(C´,k´) o H(C, k)=H₁(C₁, kk´),

o bien una traslación cuyo vector de traslación es paralelo a la línea de los centros

H´(C´,k´) o H(C, k)= T_u





Semejanzas.

Se llama semejanza de razón k a la aplicación compuesta de una homotecia de razón k y de un movimiento.

La semejanza se llama directa si la razón de la homotecia es positiva; en caso contrario, diremos que la semejanza es inversa.
 
 

Ecuaciones de una semejanza
 
Las ecuaciones de la semejanza quedan entonces como:






Volver a página principal

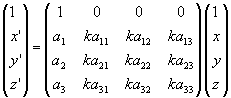
Página elaborada por: M. Teresa Pérez y Ladislao Jáñez