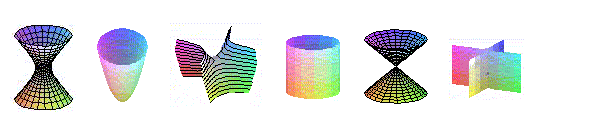
Cuádricas
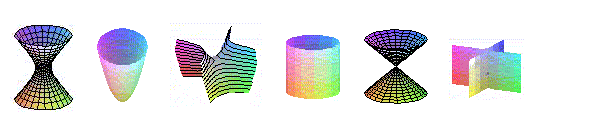
Una cuádrica es el lugar geométrico de los puntos del espacio (x,y,z) que verifican una ecuación de segundo grado del tipo
La ecuación de una cuádrica se puede escribir en forma matricial como
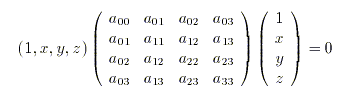
donde
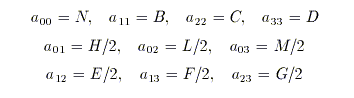
Denotaremos por 
la matriz que define la cuádrica y por
A00
la matriz adjunta del elemento
a00 en
A.
Las cuádricas se clasifican de acuerdo a su signatura
s, es decir, el módulo de la diferencia entre
el número de autovalores positivos y negativos de A00.
Sin embargo, para calcular la signatura de la cuádrica no es necesario
diagonalizar la matriz, debido a la existencia de unas cantidades invariantes
asociadas a A00 que
permiten determinar s sin necesidad de calcular
explícitamente sus autovalores. Veámoslo:
los autovalores son las raíces del polinomio característico,
es decir, las soluciones de la ecuación 
.
Ahora bien,
con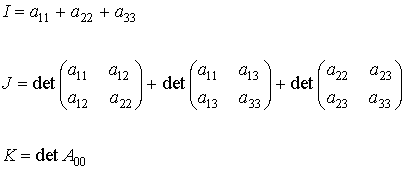
Cuando los tres autovalores de A00 son no nulos, es decir, det A00 ¹ 0, si escribimos la sucesión K, J, I, 1 y denotamos por P y V el número de permanencias y variaciones de signo que hay en ella, respectivamente, entonces |P-V| = s. Los valores I, J, K se conocen como invariantes de la cuádrica. De esta forma se tiene:
Si alguno de los autovalores es nulo (det A00 = 0) pero el determinante de A es distinto de cero, entonces;
Si det A = det A00 = 0, hay que introducir nuevos invariantes para completar la clasificación
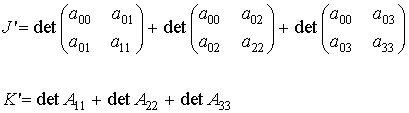
donde Aii representa la matriz adjunta del elemento aii en A para i=1,2,3.
Con estos nuevos invariantes se tiene
En la tabla siguiente se resume la clasificación anterior:
|
|
|
|||||||||||||||||||||
|
|
|
Plano polar: Dado un punto P
= (x0,y0,z0)
Î IR3
se define el plano polar de P respecto
a la cuádrica de matriz A como el plano
de ecuación
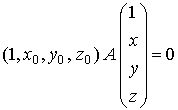
Si P pertenece a la cuádrica, entonces el plano polar de P coincide con el plano tangente a dicha superficie en P.
No todos los puntos poseen plano polar. La condición para que un punto
(x, y, z) no
lo tenga es que verifique el sistema de ecuaciones
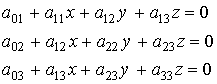
que geométricamente se interpreta como la intersección
de tres planos.
Si det A00¹
0, entonces el sistema es compatible
y tiene solución única. El punto solución se conoce como
centro de la cuádrica.
Si det A00 =
0 pueden ocurrir tres cosas,
si det A=0 y los rangos
de ambas matrices son iguales a 2 el sistema
posee una recta de soluciones, entonces se dice que la cuádrica tiene
una recta de centros. Por otro lado, si det
A=0 y el rango de ambas matrices es igual a 1
existe un plano de soluciones, y se dice que la cuádrica tiene un plano
de centros. Finalmente, si los rangos difieren o det
A ¹ 0
el sistema no tiene solución, en tal caso la cuádrica carece de
centro, recta o plano de centros.
Así, se tiene:
El centro es un punto de simetría de la cuádrica, el eje y el plano de centros son a su vez eje y plano de simetría.
Ejemplo:
Consideremos la cuádrica de ecuación
Esta cuádrica es un elipsoide (véase la tabla de clasificación).
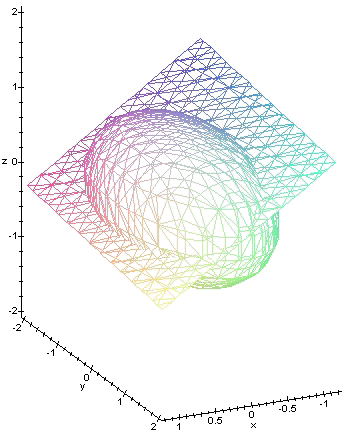
El plano polar por el punto (2, 1, 3) es el
plano de ecuación
que corta a la superficie (nótese que (2,
1, 3) es exterior a la superficie como se ve en la figura siguiente).
El centro de la cuádrica es la solución del sistema de ecuaciones
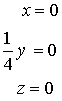
que en este caso resulta ser el origen de coordenadas.
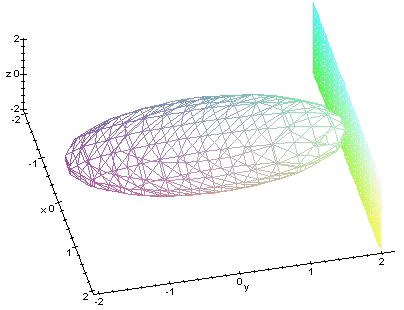
En las figuras siguientes vemos los planos polares en los puntos (0,
1, 1/2) y (0, 2, 0):
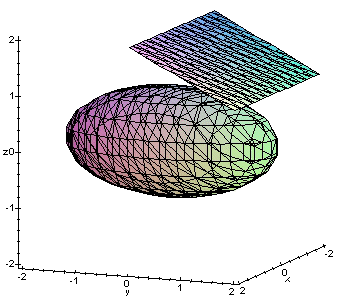
En el primer caso el punto es interior a la superficie y el plano
polar es exterior a la misma, mientras que en el segundo caso el punto e
stá sobre el elipsoide y el plano polar coincide con el plano tangente
a la superficie en dicho punto.
La ecuación reducida de una cuádrica es aquella ecuación simplificada que representa la superficie con su centro (si lo tiene) situado en el origen de coordenadas mientras que los ejes coordenados tienen relaciones particulares con la cuádrica.
Partiendo de la ecuación general de una cuádrica se puede llegar a su ecuación reducida aplicandole consecutivamente un giro y una translación de forma adecuada aunque en algunos casos especiales es necesario aplicar después de esta última un giro plano.
A continuación recogemos los tipos de ecuaciones reducidas y que cuádricas representan, así como la forma de obtenerlas a partir de los invariantes.
Denotemos por 
,
y 
las raíces de
,
entonces:
 |
 |
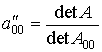
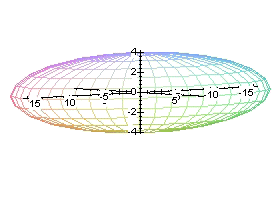
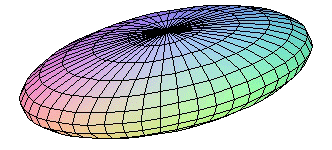
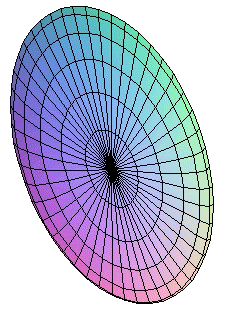
elipsoide |
hiperboloide hiperbólico |
 |
 |
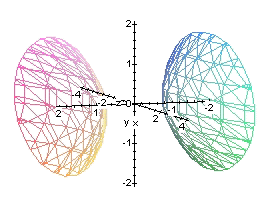hiperboloide elíptico |
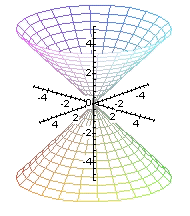
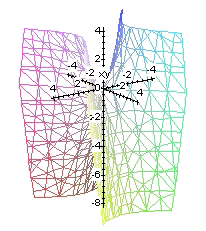
cono |
 |
 |
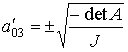
paraboloide elíptico |
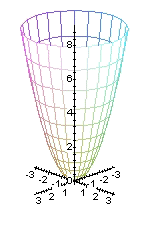
paraboloide hiperbólico |
 |
 |
 |
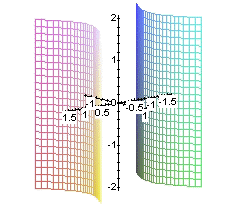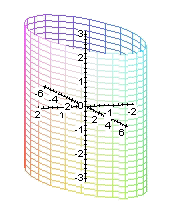
cilindro elíptico |
cilindro hiperbólico |
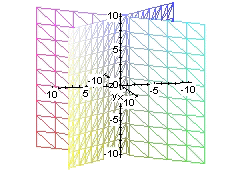
par de planos secantes |
 |
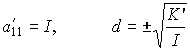
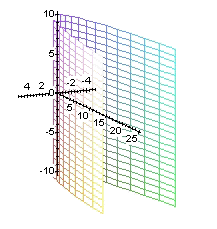cilindro parabólico |
 |
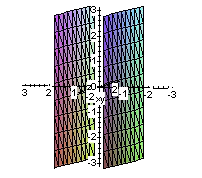par de planos paralelos |
Un ejemplo real 
Ecuación reducida:
 |
 |
 |
|
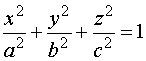La cuádrica tiene signatura 3 y los autovalores de la matriz A00
son los tres positivos.
Los cortes del elipsoide por planos paralelos a los coordenados son
curvas cónicas de tipo elipse (en lo siguiente se supone que
el elipsoide esta centrado en el origen
de coordenadas y tiene la ecuación reducida
que se da arriba):
 |
 |
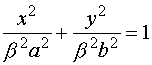
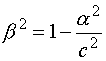
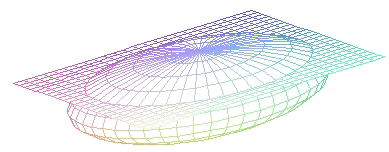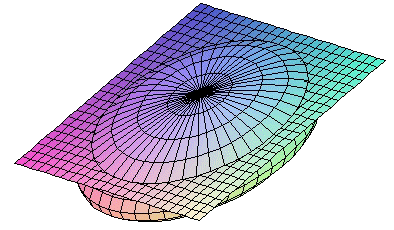Si a > c no hay intersección real.
Si a = c la intersección se reduce
a un punto, siendo el plano tangente a la superficie elíptica.
 |
 |
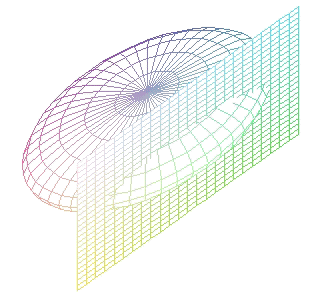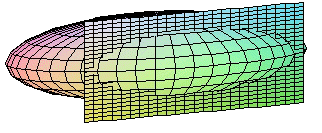(corte por un plano y = a con 0 < a < b) |
|
 |
 |
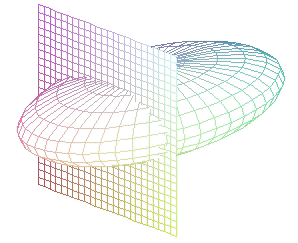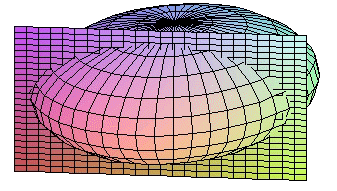(corte por un plano x = a con 0 < a < a) |
|
Un ejemplo real 
Ecuación reducida:
 |
 |
 |
 |
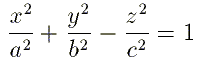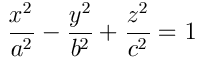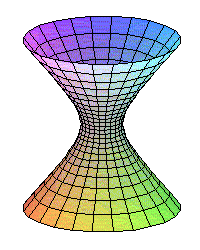
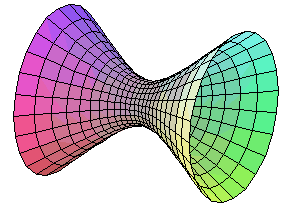
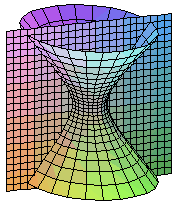
La cuádrica tiene signatura 1 y los autovalores de la matriz A00
son dos positivos y uno negativo.
Los cortes del hiperboloide por planos paralelos a los coordenados son
curvas cónicas
(en lo siguiente se supone que el hiperboloide esta centrado en el origen
de coordenadas y tiene la pimera de
las ecuaciones reducidas dadas arriba):
 |
 |
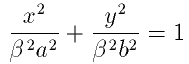
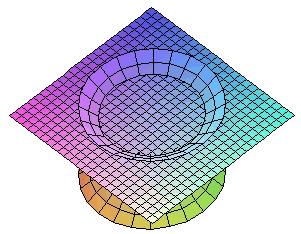( a > 0 )
|
|
 |
 |
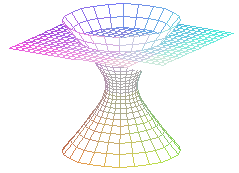
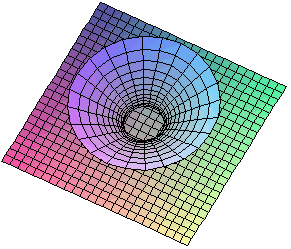( a = 0, elipse de garganta ) |
|
 |
 |
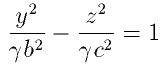
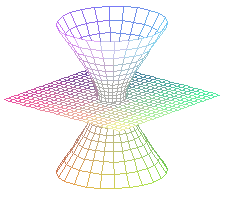
( a = 0 ) |
( a > 0 ) |
El hiperboloide hiperbólico puede ser visto también como una superficie de revolución engendrada al girar una hiperbola alrededor del eje de la cuádrica (en el caso de la ecuación reducida que estamos utilizando, el eje z) describiendo una elipse.
Además el hiperboloide hiperbólico es una superficie doblemente reglada puesto que contiene a las dos familias de rectas. Veamoslo, la ecuación del hiperboloide se puede escribir como
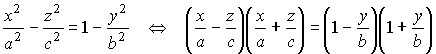
Entonces cualquier punto que satisface la ecuación del hiperboloide satisface el siguiente conjunto de ecuaciones para algun valor del parametro.
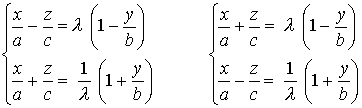
Cada una de las ecuaciones anteriores representa un plano luego finalmente tenemos un par de rectas contenidas en el hiperboloide.
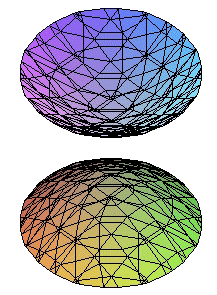
Un ejemplo real
Ecuación reducida:
 |
 |
 |
 |
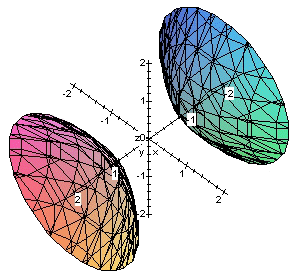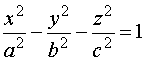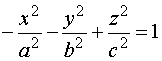(En las figuras anteriores a = b = c)
La cuádrica tiene signatura 1
y los autovalores de la matriz A00
son dos negativos y uno positivo.
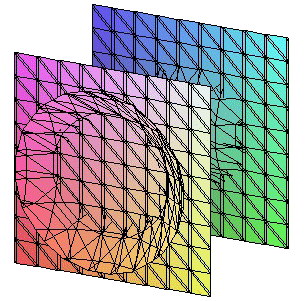
Los cortes del hiperboloide por planos paralelos a
los coordenados son curvas cónicas (El desarrollo que sigue se ha hecho utilizando la
primera de las ecuaciones reducidas)
 |
 |
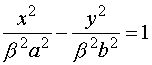
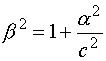
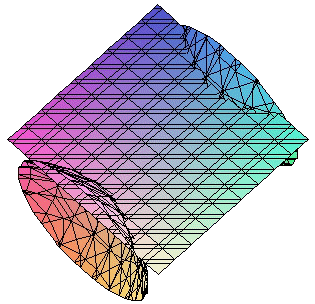
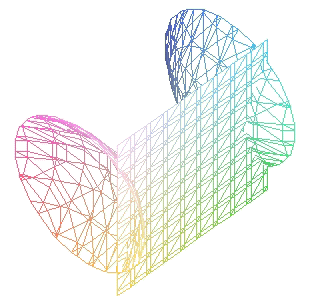
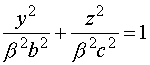
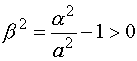
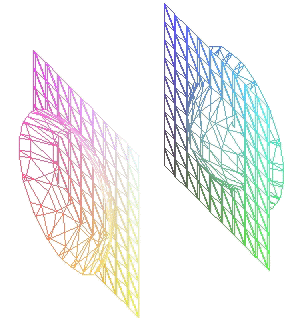x =
a > a |
x =
-a < -a |
 |
( a =
0 ) |
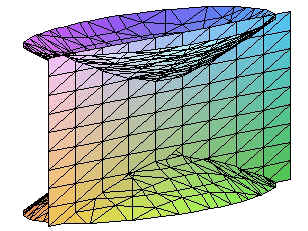
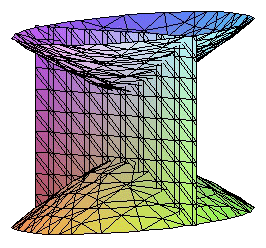
A continuación incluimos otros dibujos en los cuales el hiperboloide tiene la segunda ecuación reducida y los parámetros a,b y c son distintos
 |
 |
 |
 |
 |
 |
Un ejemplo real
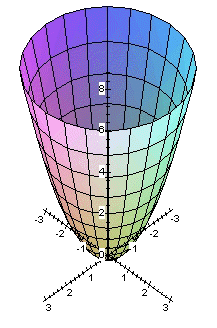
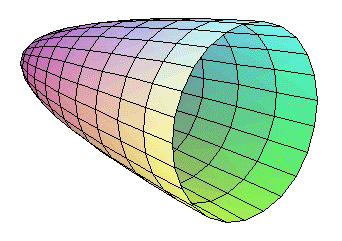
Ecuación reducida:
 |
 |
 |
 |
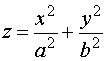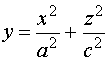Los cortes del paraboloide por planos paralelos a los coordenados son curvas cónicas, (en lo siguiente se supone que el parabolide tiene la ecuación reducida que se da arriba):
 |
 |
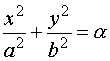
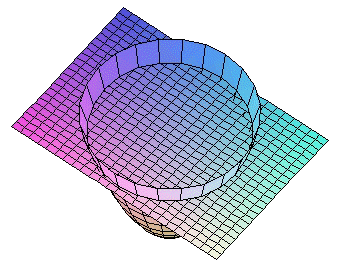( a
> 0 ) |
|
 |
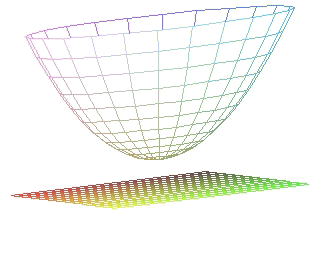(a < 0) |
 |
 |
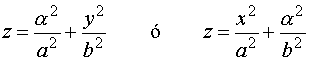
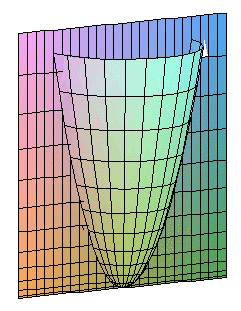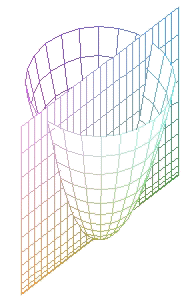(corte por plano y = a = 0 )
|
|
 |
 |
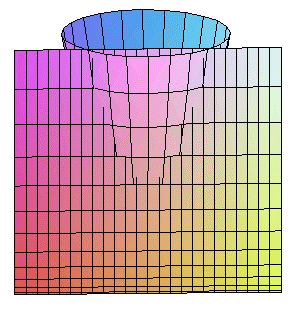(corte por plano x = a >0 ) |
|
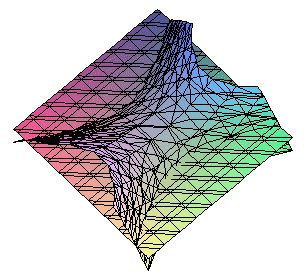
Un ejemplo real
(Foto cedida por el Prof. D. Juan M. Báez Mezquita)
Ecuación reducida:
 |
 |
 |
 |
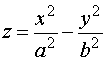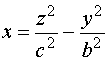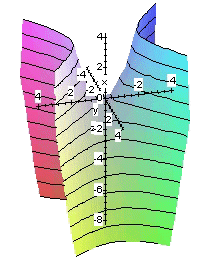
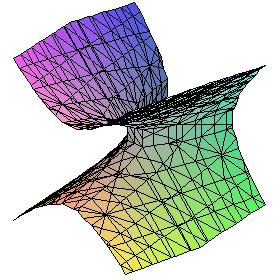
En lo que sigue utilizaremos la primera de las ecuaciones reducidas.
El paraboloide hiperbólico es una superficie doblemente reglada por las
familias de rectas:
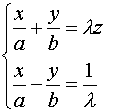
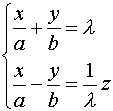
Los cortes del paraboloide por planos paralelos a los coordenados son curvas cónicas:
 |
 |
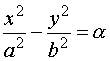
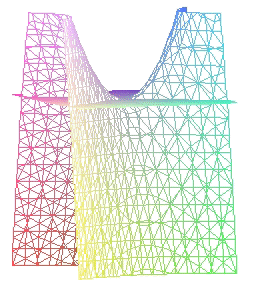
(a > 0) |
|
 |
 |
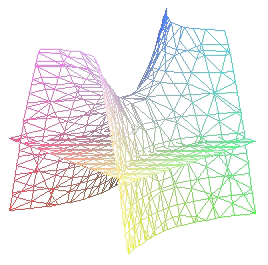(a < 0) |
|
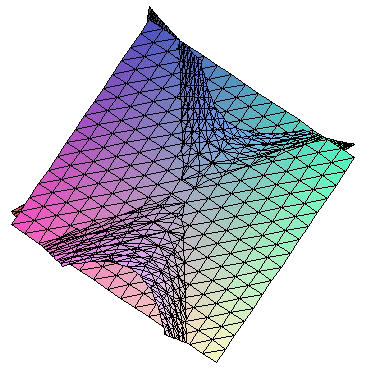
si a = 0, entonces la intersección es un par de rectas que se cortan en el origen de coordenadas
 |
 |
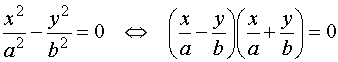
(a = 0) |
|
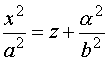y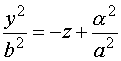 
respectivamente.  |
 |
( y = a = 0)
|
|
 |
 |
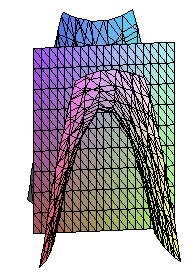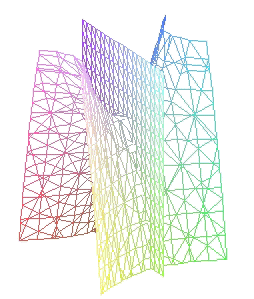( x = a = 0 ) |
|
A continuación presentamos figuras donde se ha cortado el paraboloide hiperbólico por plano oblicuos no paralelos a los coordenados
 |
 |
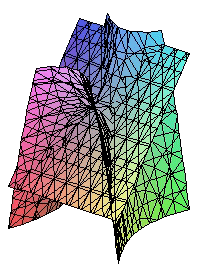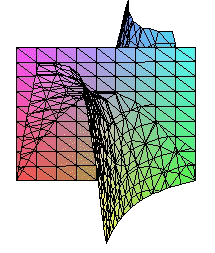Página elaborada por: M.
Teresa Pérez y Miguel A. Martín 