Una aplicación de la fórmula de Moivre

La fórmula de Moivre permite obtener de forma sencilla fórmulas trigonométricas que expresan el seno y el coseno de un ángulo múltiple en función del seno y coseno del ángulo simple. Para ello no hay más que tener en cuenta la propia fórmula de Moivre

y el desarrollo del binomio de Newton

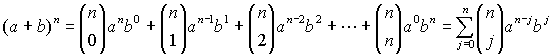
De este modo si, por ejemplo, queremos obtener una fórmula para en función del seno y del coseno de q, bastará con considerar por un lado la fórmula de Moivre

y por otro el desarrollo del cubo

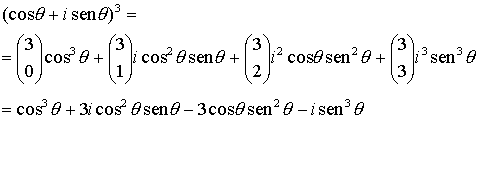
Si igualamos ahora las partes reales de ambos desarrollos tenemos

Igualando las partes imaginarias obtenemos además, sin ningún esfuerzo adicional una expresión para