Teoría
de
Códigos
 Introducción
a la teoría de códigos correctores de errores
Introducción
a la teoría de códigos correctores de errores
 Aplicaciones
técnicas
Aplicaciones
técnicas
 Antecedentes
históricos
Antecedentes
históricos
 Líneas
actuales de Investigación
Líneas
actuales de Investigación
Presentación sobre Códigos (PDF) en el I Seminario "Informática, Ciencia y
Tecnología" (2005) -- E. U. Informática de Segovia
 Volver
a Investigación
Volver
a Investigación

Códigos correctores de
errores
El modelo general de un sistema de protección contra los
errores producidos en el almacenamiento o la transmisión
de información a través de un canal discreto sin
memoria
sometido a ruido comprende los siguientes elementos:
1. Una fuente de información que genera una
cadena
o palabra de longitud k con símbolos o letras en
un
alfabetoL.
2. Un proceso de codificación que transforma
unívocamente el mensaje anterior en otro de longitud n
>
k,
sobre el mismo alfabeto u otro diferente, y al que se ha añadido
información
redundante suficiente como para poder detectar
y corregir un número razonable de errores que
puedieran producirse durante el proceso de almacenamiento o de
transmisión.
3. Un canal a través del cual se transmite
el
mensaje anteriormente codificado o en el cual se almacena dicha
información,
la cual puede sufrir algunos errores debidos al ruido existente
en dicho canal, o al deterioro del mismo en el caso de
almacenamiento en un soporte digital.
4. Un proceso de decodificación que asigna
al
mensaje distorsionado por el canal otro mensaje que, en caso de haberse
producido pocos errores, es el mensaje introducido inicialmente en
el canal, permitiéndonos así recuperar la
información
transmitida o almacenada, según el caso.
El proceso anteriormente descrito puede ser ilustrado mediante el
siguiente esquema:
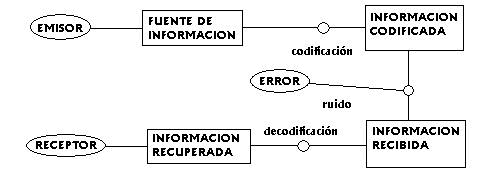
FORMALIZACION MATEMATICA
De forma más precisa, la codificación es una
aplicación inyectiva
C : Lk
----> G n
y se llama código a la imagen C de dicha
aplicación.
En el conjunto G n se define
la distancia de Hamming entre dos palabras x,y
como
d(x,y):=#{xi != yi |
i=1,...,n}
y mide el número de errores cometidos en la transmisión
cuando se recibe x en lugar de y,
dando lugar a una estructura de espacio métrico sobre G
n.
Podemos definir entonces la cantidad
d := d(C):= mín {d(x,y) | x,y
en
C, x != y}
llamada distancia mínima del código C,
y que representa el mínimo número de coordenadas
diferentes
entre dos palabras distintas cualesquiera de C.
La distancia mínima d está ligada a la capacidad
correctora del código C: éste detecta
cualquier
configuración
de hasta d-1 errores, siendo capaz de corregir
(teóricamente)
cualquier configuración de hasta (d-1)/2 errores.
El caso que consideraremos en adelante es aquél en que L=G=Fq
es un cuerpo finito de cardinal q,
y la codificación C
es una aplicación Fq-lineal, en cuyo caso
diremos
que C es un código lineal de
longitud n y dimensión k, que
junto
con la distancia d constituyen sus parámetros
fundamentales.
Se dice entonces que C es de tipo [n,k,d]q
.
Asimismo, se llaman parámetros asintóticos de C
al par [R,d], donde R := k/n
se llama tasa de transmisión y
representa simultáneamente el coste y la velocidad de
transmisión,
y donde d := d/n se llama distancia
relativa y
mide la capacidad correctora en relación a su longitud.
Finalmente,
se llama redundancia a la diferencia n-k.
Ejemplos:
* El código de repetición (a,b,c,d) --->
(a,b,c,d,a,b,c,d)
es de tipo [8,4,2]q ;
por tanto, detecta 1 error, aunque no lo pueda corregir.
* El código de repetición (a,b,c,d) --->
(a,b,c,d,a,b,c,d,a,b,c,d)
es de tipo [12,4,3]q ;
por tanto, detecta 2 errores y corrige 1 error.
* El código de Hamming binario con matriz de control
0001111
0110011
1010101
es de tipo [7,4,3]2 ; por tanto, también detecta
2 errores y corrige 1, pero con mejor tasa de transmisión.
Si C es un código lineal, se dice que G es
una
matriz generatriz de C si es de tipo n x k
y sus filas forman una base de C
como subespacio de Fqn ; si fijamos una
matriz generatriz G, la operación de codificación
puede describirse en forma matricial
como c = m . G, donde m eFqk
es la información que queremos codificar. Si la matriz G
es de la forma G=(Ik | M),
donde Ik es la matriz identidad de dimensión
k,
se dice que C es un código en forma estándar
;
en este caso, los k primeros
símbolos de una palabra código se denominan símbolos
de información, y los restantes se denominan símbolos
de control.
La codificación de un código estándar es muy
sencilla,
puesto que consiste en añadir al mensaje m los
símbolos
de control
m . M, y un ejemplo típico es el llamado código
de Hamming.
Se dice que una matriz H de tipo (n-k) x n
de rango máximo es una matriz de control del
código
C
si la aplicación lineal dada por
SH(x) := x . Ht
tiene
a C como núcleo; en este caso, podemos describir C
como
C = { x e Fqn
| x . Ht = 0 }
El código dual C* de un código lineal C
se define como el subespacio ortogonal de C relativo a la forma
bilineal simétrica no degenerada
Fqn x Fqn
----> F
dada por
<x,y> := x . yt
Una matriz generatriz de C* es una matriz de control para C,
y viceversa.
Referencias:
[1]: C. Munuera
y
J. Tena, "Codificación de la Información",
Publicaciones de la Universidad de Valladolid, Ciencias nº 25 (1997).
[2]: H. Imai,
"Essentials
of error-control coding techniques",
Academic Press, Inc. (1990).
 Volver
al Indice
Volver
al Indice

Aplicaciones técnicas
SISTEMAS DE COMUNICACION
-
Comunicación Vía Satélite.
-
Broadcasting (radio y TV digital).
-
Sistemas de Teletexto.
-
Telecomunicaciones (telefonía digital).
SISTEMAS INFORMATICOS
-
Circuitos lógicos.
-
Memorias de Semiconductores.
-
Discos magnéticos (HD).
-
Discos de lectura óptica (CD-ROM).
SISTEMAS DE AUDIO Y VIDEO
-
Sonido Digital (CD).
-
Video Digital (DVD).
En la siguiente página web se puede encontrar una interesante
demostración práctica de corrección de errores:
Reed
Solomon en-/decoding and decoding in DVD
 Volver
al Indice
Volver
al Indice

Antecedentes históricos
El origen de la teoría de códigos correctores
de errores se encuentra en los trabajos de Golay, Hamming y Shannon
hacia mediados del presente siglo, tanto en su vertiente probabilista
como en la algebraica, y desde su inicio
el tema ha sido siempre un problema de ingeniería, con
aplicación
tanto en la transmisión de información
(ingeniería de telecomunicaciones) como en el almacenamiento
de la misma en soporte digital (ingeniería
informática),
siendo su finalidad el preservar la calidad de la información
y las comunicaciones contra la amenaza del ruido, la distorsión
o el deterioro del medio. No obstante, el desarrollo de dicha
teoría
se ha realizado gracias a la utilización de técnicas
matemáticas
cada vez más sofisticadas; estas técnicas recorren
múltiples
campos de la matemática, que van desde la teoría de
probabilidades,
el cálculo combinatorio o el álgebra lineal hasta la
aritmética, la teoría de cuerpos o la geometría
algebraica.
En un principio, la teoría empezó con un enfoque
esencialmente
probabilístico con la teoría de Shannon, pero
pasó
posteriormente a un enfoque más algebraico, surgiendo entonces
muchos ejemplos prácticos (aún en uso hoy en día)
como los códigos de Golay y de Hamming, los códigos
cíclicos y BCH, o los códigos de Reed-Solomon
y de Reed-Muller.
Finalmente, la introducción en los años 70 por Goppa
de una nueva construcción de códigos lineales a partir de
curvas algebraicas lisas
(llamados códigos geométricos de Goppa o
códigos
álgebro-geométricos) cambió por completo el
panorama
de investigación
en el terreno de la teoría de códigos correctores de
errores; por un lado, la codificación de dichos
códigos
parecía sencilla
(aunque tan clara como en el caso de los códigos lineales
clásicos),
y por otro sus parámetros podían ser
fácilmente
controlables
a partir de fórmulas clásicas de la geometría
algebraica (tales como el teorema de Riemann-Roch). Además,
dicha teoría permitió
en los años 80 la construcción explícita de
familias
de códigos cuyos parámetros sobrepasan
asintóticamente
la cota de
Varshamov-Gilbert, y en consecuencia dar una solución
efectiva (y con complejidad polinomial) al problema principal
de la teoría de códigos, que fue considerado por
Shannon en términos puramente probabilísticos pero sin
ninguna
idea constructiva.
A pesar del interés que suscitó el estudio de los
códigos
geométricos de Goppa desde su origen, no pudieron encontrarse
algoritmos eficientes para su decodificación
hasta
finales de los años 80, gracias a sucesivos trabajos de
Justesen et al., Skorobogatov y Vladut, y Porter
(recomendamos [1] como una buena lectura introductoria).
Estos métodos están lejos de la capacidad correctora
de los códigos a los que se aplican, y algunos de ellos
requieren condiciones restrictivas respecto al tipo de códigos
que pueden utilizarse, pero algunos años más tarde
surgieron nuevos métodos que resolvieron este problema de una
forma efectiva, como es el caso de los algoritmos de
Ehrhard o Duursma. En la actualidad se desarrollan
algoritmos
más rápidos y eficientes (a costa de perder algo de
generalidad),
basados en el esquema de decodificación mayoritaria de Feng
y Rao, que utilizan o bien relaciones de recurrencia lineal
(como el algoritmo de Sakata) o bien bases de Gröbner
(como
el de Saints y Heegard).
No obstante, los códigos AG
(álgebro-geométricos)
apenas han sido implementados en la práctica por los ingenieros
debido a la
profundidad matemática de las ideas subyacentes. Por este
motivo,
los matemáticos están haciendo actualmente una
descripción
de este tipo de códigos y de su tratamiento práctico
mediante una aproximación más elemental
(ver
[2]).
Por otra parte, aunque los parámetros de los
códigos
AG son mucho mejores que los clásicos
en sentido asintótico
(es decir, para códigos de longitud arbitrariamente grande),
las aplicaciones técnicas no se han visto aún en la
necesidad
práctica de
sustituir los códigos que actualmente se utilizan por otros
de mayor longitud sin que se dispare simultáneamente el coste y
la tasa de error.
Como contrapartida, los códigos clásicos que actualmente
se utilizan tienen una decodificación bastante
más
rápida y efectiva.
Por último, aunque algunos de los métodos de
decodificación
para códigos geométricos de Goppa son efectivos, su preprocesamiento
es de una elevada dificultad e involucra complejos algoritmos basados
en métodos de la geometría algebraica computacional.
Por ejemplo, en los algoritmos de decodificación que hoy en
día se consideran más eficientes, se ve involucrado el
cálculo
de semigrupos de Weierstrass y su distancia de Feng-Rao,
o los algoritmos de Hamburger-Noether y de Brill-Noether.
Por último, decir que el estudio de la teoría de
códigos
está íntimamente ligado a una serie de tópicos
propios
de la matemática discreta
tales como retículos, empaquetamientos de esferas, sumas
exponenciales,
la teoría de grafos o la geometría aritmética,
así
como otra serie
de temas de procedencia variada tales como la teoría de la
información, la criptografía,
el álgebra computacional o la teoría
de la señal.
Referencias:
[1]: T. Hoeholdt
and R. Pellikaan, "On the decoding of algebraic-geometric codes",
IEEE Trans. Inform. Theory 41, pp. 1589-1614 (1995).
[2]: T. Hoeholdt,
J.H.
van Lint and R. Pellikaan, "Algebraic Geometry codes",
in the Handbook of Coding Theory, vol. 1, pp. 871-961, ed.
Elsevier-Amsterdam
(1998).
 Volver
al Indice
Volver
al Indice

Líneas actuales de
Investigación
En el terreno de los códigos AG, la investigación
matemática se centra actualmente entorno a los siguientes problemas
:
 Construcción
explícita de sucesiones de códigos que sobrepasen la cota
de Varhsamov-Gilbert, mediante la
Construcción
explícita de sucesiones de códigos que sobrepasen la cota
de Varhsamov-Gilbert, mediante la
construcción previa de torres de cuerpos de funciones racionales
que alcancen la cota de Drinfeld-Vladut.
 Construcción
y decodificación efectivas de los códigos AG, con el fin
de poder implementar los códigos
Construcción
y decodificación efectivas de los códigos AG, con el fin
de poder implementar los códigos
obtenidos en el apartado anterior, mediante técnicas de
"Geometría
Algebraica Computacional".
 Estudio de los
llamados "improved AG codes" (códigos AG mejorados) a partir de
técnicas elementales
Estudio de los
llamados "improved AG codes" (códigos AG mejorados) a partir de
técnicas elementales
de álgebra abstracta, que permitan llevar a la práctica
real los códigos AG "sin Geometría Algebraica".
 Decodificación
rápida de los códigos AG "sobre un punto", con el fin de
aproximarse a la complejidad de los
Decodificación
rápida de los códigos AG "sobre un punto", con el fin de
aproximarse a la complejidad de los
códigos actualmente utilizados, mediante técnicas de
"relaciones de recurrencia" y "bases de Groebner".
En cuanto a mis líneas de investigación actuales, se
encuentran
las siguientes:
 Construcción
efectiva de códigos AG mediante los algoritmos de Hamburger-Noether,
Brill-Noether,
Construcción
efectiva de códigos AG mediante los algoritmos de Hamburger-Noether,
Brill-Noether,
Abhyankar-Moh y el algoritmo de la base entera.
 Cálculo
de la distancia de Feng y Rao de semigrupos de Weierstrass como
estimación de la distancia mínima
Cálculo
de la distancia de Feng y Rao de semigrupos de Weierstrass como
estimación de la distancia mínima
en los "códigos AG sobre un punto" (one-point AG codes), para
el caso de semigrupos simétricos, telescópicos,
intersección completa y Arf, así como las
sucesivas distancias generalizadas.
 Estudio
del comportamiento asintótico de sucesiones de curvas reducidas,
no necesariamente irreducibles,
Estudio
del comportamiento asintótico de sucesiones de curvas reducidas,
no necesariamente irreducibles,
mediante la construcción explícita de ejemplos con
modelos
planos y su aplicación al problema principal de la
Teoría de Códigos.
 Decodificación
de los códigos AG en términos de una ecuación
clave,
mediante la incorporación de un
Decodificación
de los códigos AG en términos de una ecuación
clave,
mediante la incorporación de un
esquema de mayoría análogo al caso del algortimo
de Feng y Rao.
A continuación escribo algunos links interesantes
relacionados con el tema:
-
Universidad Tecnológica de Eindhoven
(Holanda).
-
Universidad Tecnológica de Dinamarca (DTU)
en Copenhague.
-
Instituto de Matemática Pura y Aplicada (IMPA)
en Brasil.
-
Universidad Nacional Autónoma de México.
-
Servidores URL de Matemáticas.
 Volver
al Indice
Volver
al Indice

 Buzón
de sugerencias
Buzón
de sugerencias
![]()
![]() Introducción
a la teoría de códigos correctores de errores
Introducción
a la teoría de códigos correctores de errores![]()
![]() Aplicaciones
técnicas
Aplicaciones
técnicas![]()
![]() Antecedentes
históricos
Antecedentes
históricos![]()
![]() Líneas
actuales de Investigación
Líneas
actuales de Investigación![]()
![]()

![]()