Siguiente: Sobre este documento... Subir: Estructuras algebraicas Anterior: Cuerpo
Un retículo es una terna
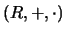 tal que:
tal que:
- Ambas operaciones son asociativas.
- Ambas operaciones son conmutativas.
- Se verifican las `` Leyes de Absorción'' (o simplificativas):
De las propiedades anteriores se deducen las de idempotencia
Si se verifican las dos propiedades distributivas (de cada una de las
operaciones con respecto de la otra) se trata de un retículo distributivo.
Por otra parte, si existen elementos llamados 0 y 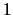 tales que
se dice que es un retículo acotado.
Si además de ser acotado, el retículo verifica que
se trata de un retículo complementario
(
tales que
se dice que es un retículo acotado.
Si además de ser acotado, el retículo verifica que
se trata de un retículo complementario
(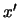 se llama complementario de
se llama complementario de 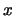 ).
Por último, y aunque lo estudiaremos aparte con una definición
`` minimal'' (es decir, incluyendo en la definición
el mínimo número posible de propiedades), diremos que a un retículo
distributivo y complementario se le llama álgebra de Boole.
Por ejemplo, el retículo
).
Por último, y aunque lo estudiaremos aparte con una definición
`` minimal'' (es decir, incluyendo en la definición
el mínimo número posible de propiedades), diremos que a un retículo
distributivo y complementario se le llama álgebra de Boole.
Por ejemplo, el retículo
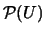 anteriormente citado es,
de hecho, un álgebra de Boole.
anteriormente citado es,
de hecho, un álgebra de Boole.
Siguiente: Sobre este documento... Subir: Estructuras algebraicas Anterior: Cuerpo
Jose Ignacio Farran Martin
2003-07-16